bayesian networks 🔗

markov blanket 🔗

Source: Barber’s BRML:

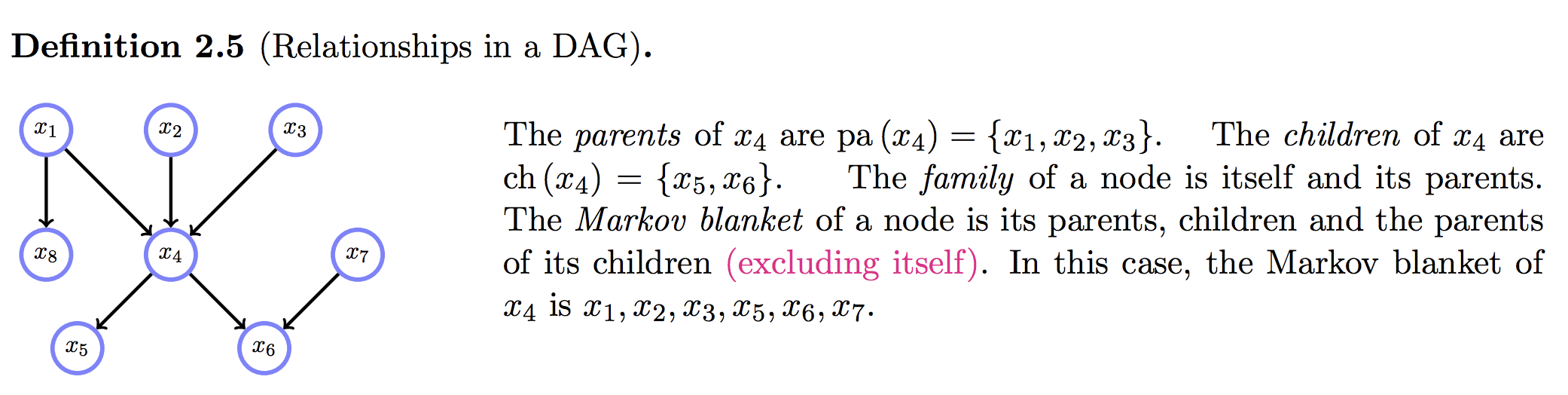
d-separation 🔗

tl;dr 🔗

Active paths (source) 🔗

• Simple case: empty conditioning set

  Consider

  1. A -> C -> B
  2. A <- C <- B
  3. A <- C -> B
  4. A -> C <- B

  If interpreted causally,

  1. A indirectly causes B
  2. B indirectly causes A
  3. C is a common cause of A and B

  All of the first three causal situations give rise to association, or dependence, between A and B => active paths. However, in case 4, A and B have a common effect in C but no causal connection between them; C is called a collider. Intuitively, non-colliders transmit information (dependence) while non-colliders don’t. When the conditioning set is empty, d-separation is a simple matter of whether there are any paths between X and Y with no colliders (active).

• C in conditioning set

  Now C’s active-ness flip-flops. Conditioning on C makes A and B independent for the first 3 cases; C is now inactive.

  1. and 2.: Conditioning on C blocks the path from A to B.

  3: Conditioning on a common cause C makes its effects, A and B, independent of each other. For the 4th case, C is now active when it’s in the conditioning set. E.g. dead battery -> car won’t start <- no gas Knowing about the battery says nothing about the gas, but FIRST knowing that the car won’t start and then knowing about the battery tells you that there’s no gas. So, independent causes are made dependent by conditioning on a common effect (car won’t start). Finally, if conditioning on a collider activates the path, so does conditioning on any of its descendants.

the multivariate Gaussian distribution 🔗

comparing gaussian quadratic form to obtain mean and covariance, instead of completing the square 🔗

Source: Bishop’s PRML chapter 2.3