Slides are available here, made from the same org file that this Hugo blogpost was generated from.
Membership Inference Attacks against Machine Learning Models 🔗
Reza Shokri, Marco Stronati, Congzheng Song, and Vitaly Shmatikov (2017)
Presented by Christabella Irwanto
Machine learning as a service 🔗
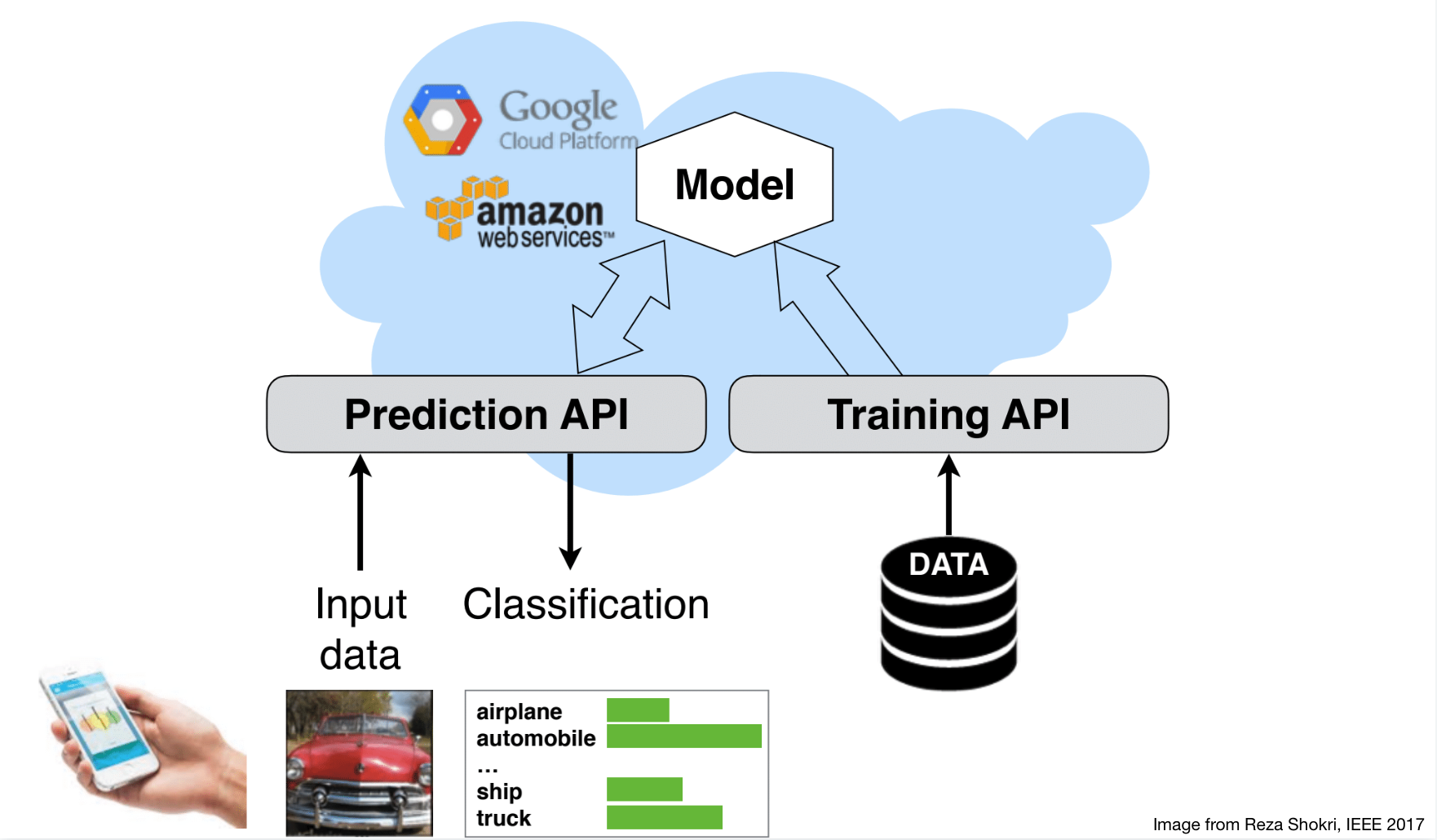
The elements of output vector are in [0, 1] and sum up to 1.
Machine learning privacy 🔗
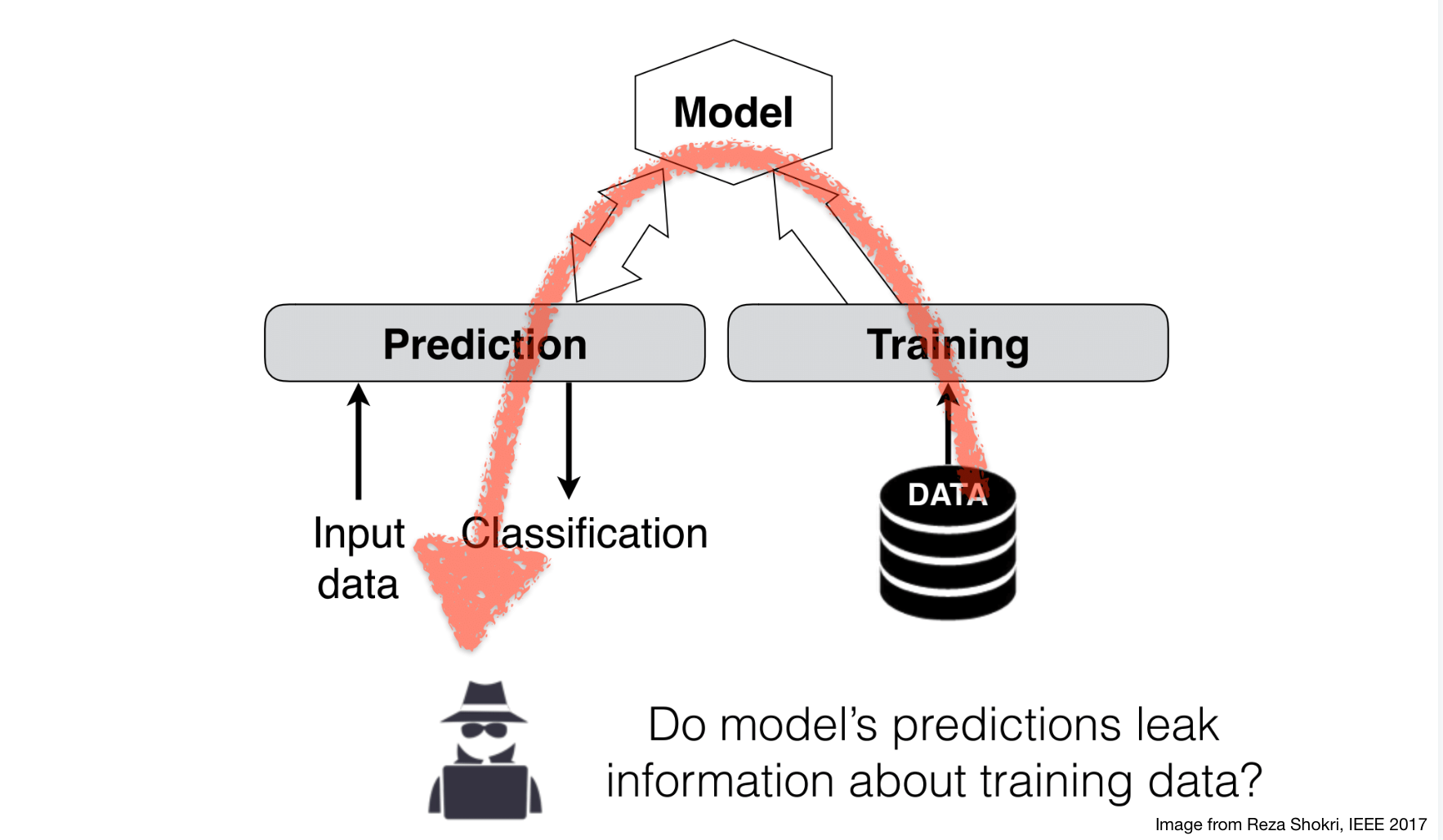
In the context of the overall ML pipeline, we are considering a malicious client
Basic membership inference attack 🔗
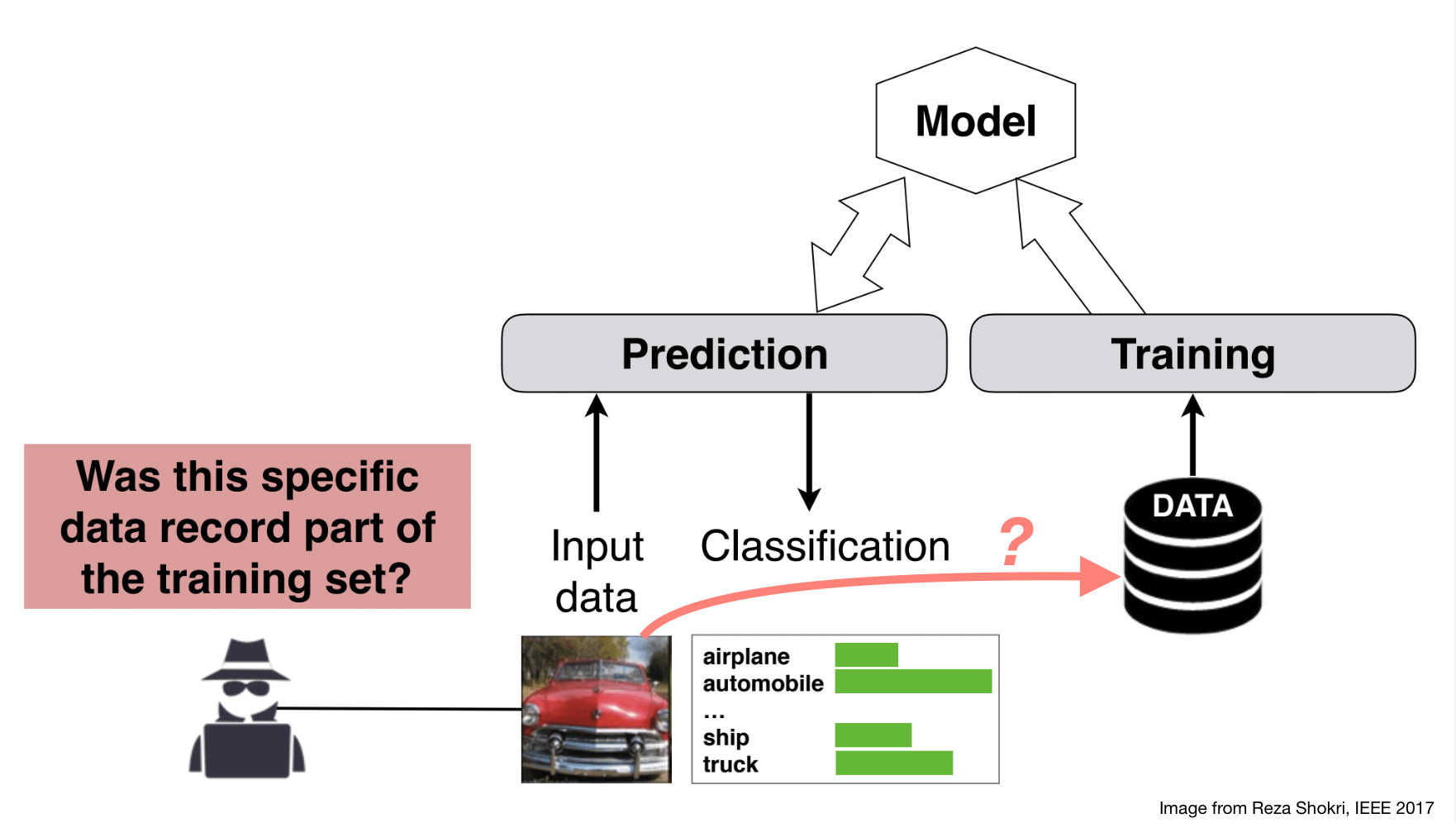 E.g. patients’ clinical records in disease-related models.
E.g. patients’ clinical records in disease-related models.
Adversary model 🔗
- 😈 Who: malicious client
- 🕔 Attack time: inference
- 🥅 Goal: compromise training data privacy
- determine if a data record \(\mathbf{x}\) was in the model \(f_{target}\)’s (sensitive) training dataset \(D^{train}_{target}\)
- 💪 Capability:
- labeled data record \((\mathbf{x}, y)\)
- model query access to obtain prediction vector \(\mathbf{y}\) for \(\mathbf{x}\)
- format of inputs and outputs, e.g. shape and range of values
- either
- (1) architecture and training algorithm of model, or
- (2) black-box access to the oracle (e.g., a “ML as a service” platform) that was used to train the model
Key contributions 🔑 🔗
- Turn membership inference into a binary classification problem
- Invent “shadow training technique” to mimic black-box models
- Develop 3 effective methods to generate training data for the shadow models
- Evaluate membership inference techniques against neural networks, Amazon ML, and Google Prediction API on realistic tasks successfully
- Quantify how membership leakage relates to performance and overfitting
- Evaluate mitigation strategies
Membership inference approach 🔗
For a given labeled data record \((\mathbf{x}, y)\) and a model \(f\)’s prediction vector \(\mathbf{y} = f(\mathbf{x})\), determine if \((\mathbf{x}, y)\) was in the model’s training dataset \(D^{train}_{target}\)
How is this even possible? 🔗
- Intuition: machine learning models often behave differently on data that they were trained on 🐵 versus “unseen” data 🙈
- Overfitting is one of the reasons
- We can construct an attack model that learns this behaviour difference
End-to-end attack process 🔗
- With labeled record \((\mathbf{x}, y)\), use target model \(f_{target}\) to compute prediction vector \(\mathbf{y} = f_{target}(\mathbf{x})\)
- Attack model \(f_{attack}\) receives both true class label \(y\) and \(\mathbf{y}\)
- We need \(y\) since \(\mathbf{y}\)’s distribution depends heavily on it
- \(f_{attack}\) computes membership probability \(Pr{(\mathbf{x}, y) \in D^{train}_{target}}\)
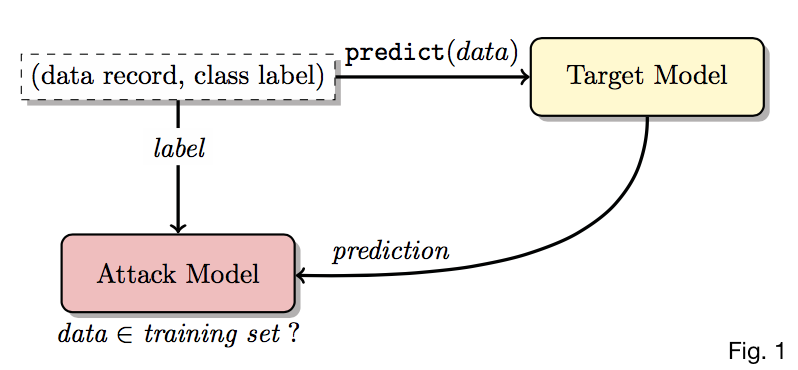
How to train \(f_{attack}\) without detailed knowledge of \(f_{target}\) or its training set? 🔗
- Mimic target model with “shadow models”
- Train shadow models on proxy targets for which we will know the membership ground truth
- Becomes supervised training
- A binary classification task predicting “in” or “out”
Shadow models 🔗
- \(k\) shadow models, each \(f^i_{shadow}\) trained on dataset \(D^{train}_{shadow^i}\) of same format and similar distribution as \(D^{train}_{target}\)
- Assume worst case performance that \(\forall i, D^{train}_{shadow^i} \bigcap D^{train}_{target} = \emptyset\)
- \(\uparrow k \implies \uparrow\) training fodder for \(f_{attack} \implies \uparrow\) accuracy of \(f_{attack}\)
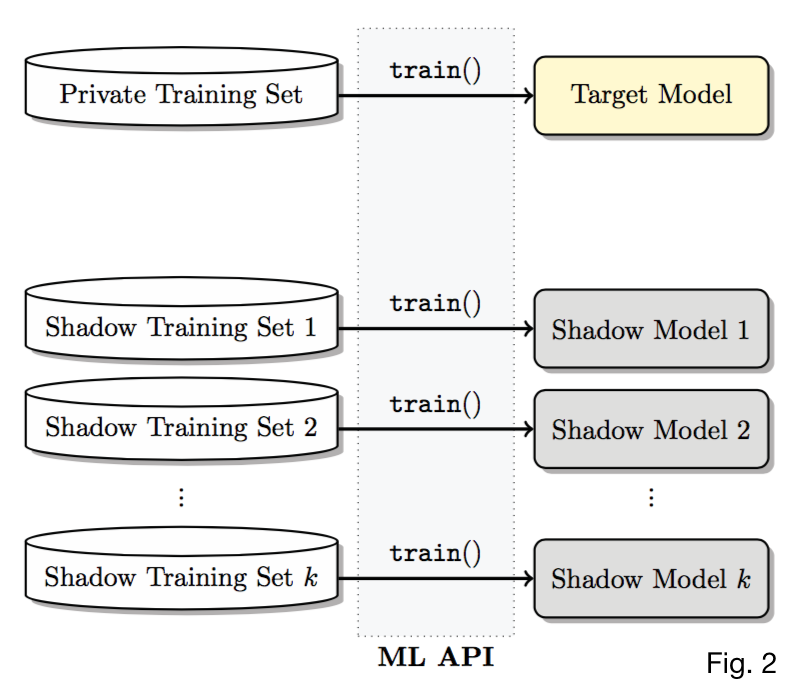
Any overlap and the attack will perform better
- The training datasets of the shadow models may overlap.
- Shadow models must be trained similarly to target model, either with same training algorithm and model structure if known, or with the same ML service.
- All models’ internal parameters are trained independently.
Synthesizing datasets for \(f_{shadow}\) 🔗
- Model-based synthesis: Synthesize high confidence records on \(f_{target}\) from noise with hill-climbing search and sampling
- Statistics-based synthesis: Requires statistical information about the population from which \(D^{training}_{target}\) was drawn
- Simulated by independently sampling from marginal distributions of each feature
- Noisy real data: Real data from a different population or sampled non-uniformly
- Simulated by flipping binary values of 10% or 20% randomly selected features
Model-based synthesis 🔗

- (1) Search the space of possible data records to find high confidence inputs, and (2) sample from these records.
- Initialization values sampled uniformly at random from entire possible range.
- Hill-climbing objective
- not met: \(k\) features randomized again
- met, but not sufficient: add to rejections count and reduce \(k\) if too many rejects
- controls diameter of search around accepted record
- met, and sufficient: select record with probability \(y_c\)
Training dataset for \(f_{attack}\) 🔗
- Query each \(f^i_{shadow}\) with \(D^{train}_{shadow^i}\) and a disjoint \(D^{test}_{shadow^i}\).
- \(\forall (\mathbf{x}, y) \in D^{train}_{shadow^i}\), get \(\mathbf{y} = f^i_{shadow}(\mathbf{x})\) and add \((y, \mathbf{y}, \text{in})\) to \(D^{train}_{attack}\)
- \(\forall (\mathbf{x}, y) \in D^{test}_{shadow^i}\), get \(\mathbf{y} = f^i_{shadow}(\mathbf{x})\) and add \((y, \mathbf{y}, \text{out})\) to \(D^{train}_{attack}\)
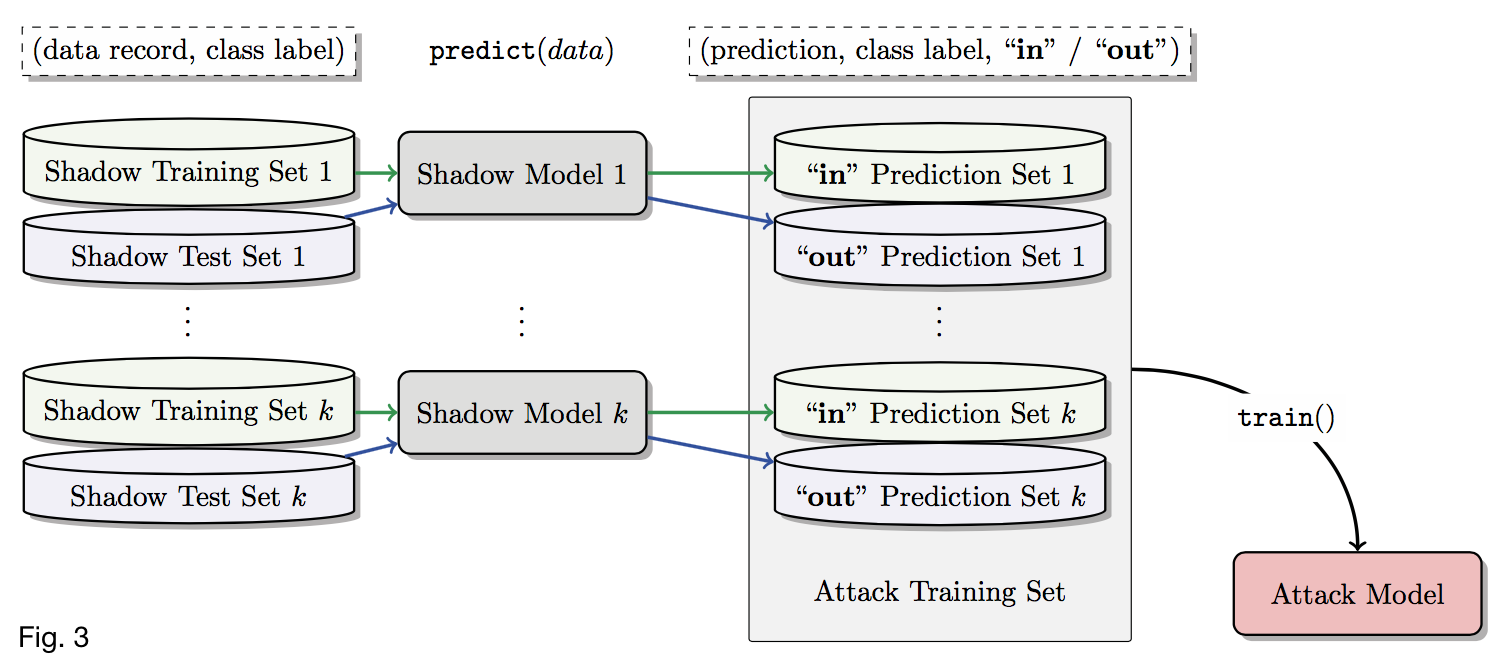
Training \(f_{attack}\) 🔗
- Partition \(D^{train}_{attack}\) by class and train a separate model for each class label \(y\)
- Given \(\mathbf{x}\) and \(\mathbf{y}\), predict membership status (“in” or “out”) for \(\mathbf{x}\)
- Class-specific models \(\uparrow\) accuracy because the true class heavily influences the target model’s behaviour (produces different output distributions)
If using method 1, model-based synthesis, the records used in both \(D^{training}_{target}\) and \(D^{test}_{target}\) have high confidence
- \(\implies\) \(f_{attack}\) does not simply learn to classify “in” vs “out” based on high confidence, but performs a much subtler task
- Method-agnostic: can use any state-of-the-art machine learning framework or service to build the attack model
Experiments 🔗
- Datasets for classification
- CIFAR-10 and CIFAR-100: 32x32 color images
- Shopping purchases to predict shopping style: 600 binary features
- Performed clustering into different number of classes {2, 10, 20, 50, 100}
- Foursquare check-ins to predict geosocial type: 446 binary features
- Texas hospital stays to predict procedure: 6,170 binary features
- MNIST: 32 x 32 monochrome images
- UCI Adult (Census Income): predict if annual income exceeds $50K
- Target models
- Google Prediction API: No configurations
- Amazon ML: A few tweakable metaparameters; authors test defaults and one other configuration
- Standard CNN for CIFAR and standard fully-connected neural network for purchases
Evaluation methodology 🔗
- Equal number of members (“in”) and non-members (“out”) to maximize uncertainty of inference; baseline accuracy is 0.5
- Metrics
- ✅ Precision: what fraction of records inferred as members are indeed members
- ☂ Recall: coverage, i.e. what fraction of members are correctly inferred
- Training datasets for different shadow models may overlap
Results 🔗
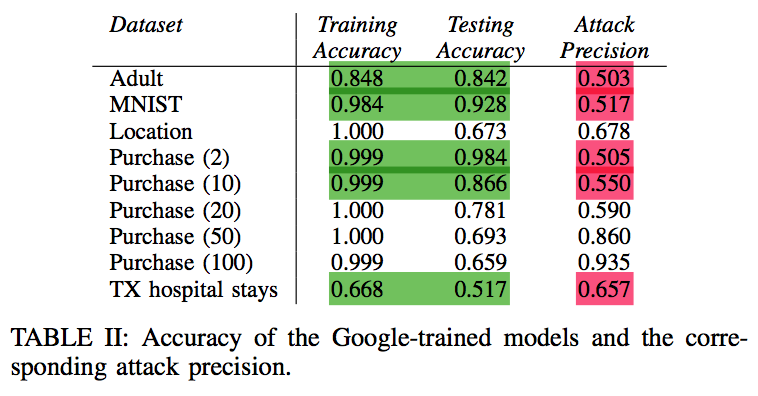
Effect of overfitting 🔗
- Large gaps between training and test accuracy \(\implies\) overfitting
- Larger test accuracy \(\implies\) 👍 generalizability, predictive power
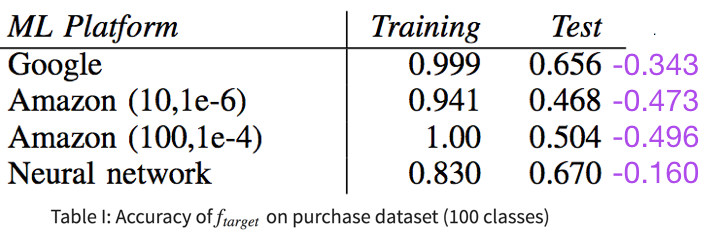
- \(\uparrow\) overfitting, \(\uparrow\) leakage (Fig. 11)… but only for same model type
- Amazon (100, 1e − 4) overfits and leaks more than Amazon (10, 1e − 6)
- But Google leaks more than both Amazon models, even if it is less overfitted and has generalizability
- Overfitting is not the only factor in vulnerability; different model structures “remember” different amounts of information
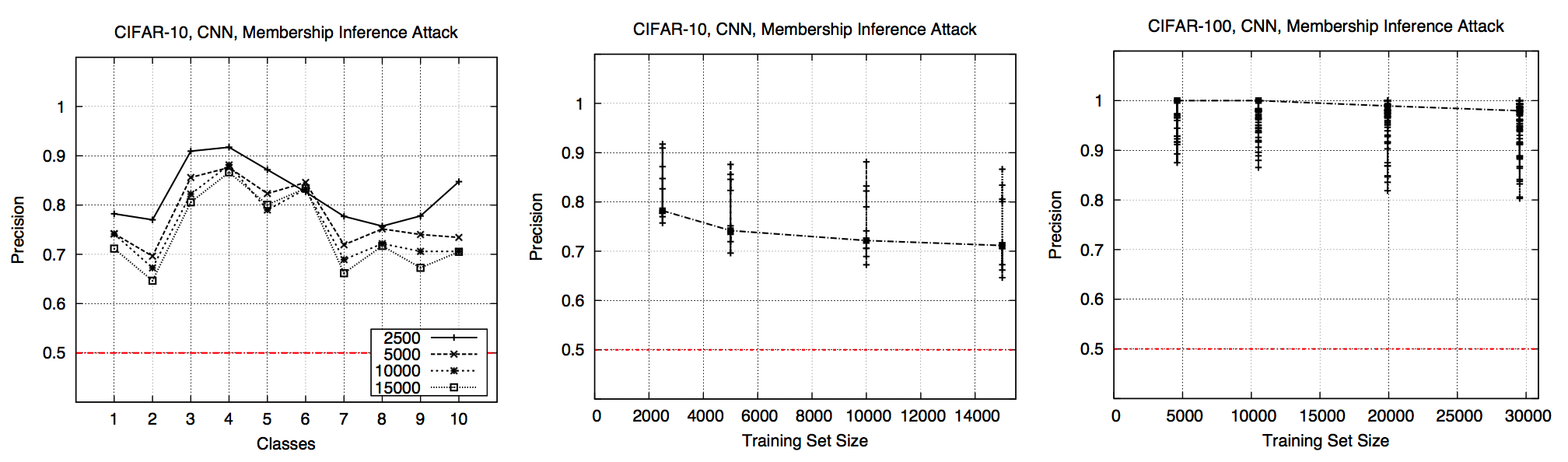
Precision on CIFAR against CNN (Fig. 4) 🔗
- Low accuracies (0.6 and 0.2) \(\implies\) heavily overfitted
- Precision follows the same pattern across all classes
- \(\uparrow\) training dataset size, \(\uparrow\) variance across classes and \(\downarrow\) precision
- Attack performs much better than baseline, especially CIFAR-100
- The more classes, the more leakage because models need to “remember” more about training data
- CIFAR-100 is more overfitted to training dataset
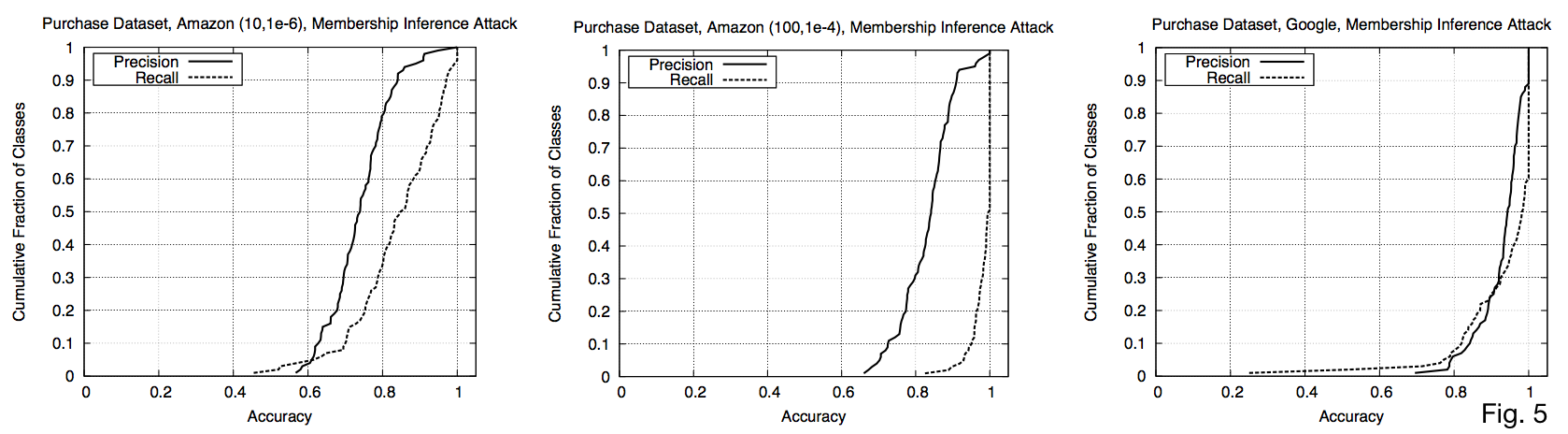
Precision on Purchase Dataset against all target models 🔗
- Any point shows cumulative fraction of classes in y for which the attacker can obtain a membership inference precision up to x
- 50, 75, 90-percentiles of precision are (0.74, 0.79, 0.84), (0.84, 0.88, 0.91), and (0.94, 0.97, 1) respectively
- E.g. 50% of classes get up to 0.74 precision for Amazon
- Recall is close to 1 on all
Failure modes 🔗
- Failed on MNIST (0.517 precision) because of small number of classes and lack of randomness in data in each class
- Failed on Adult dataset, because
- Model is not overfitted
- Model is binary classifier, so attacker essentially has only has 1 signal to infer membership on
Effect of noisy shadow data on precision (Fig. 8) 🔗
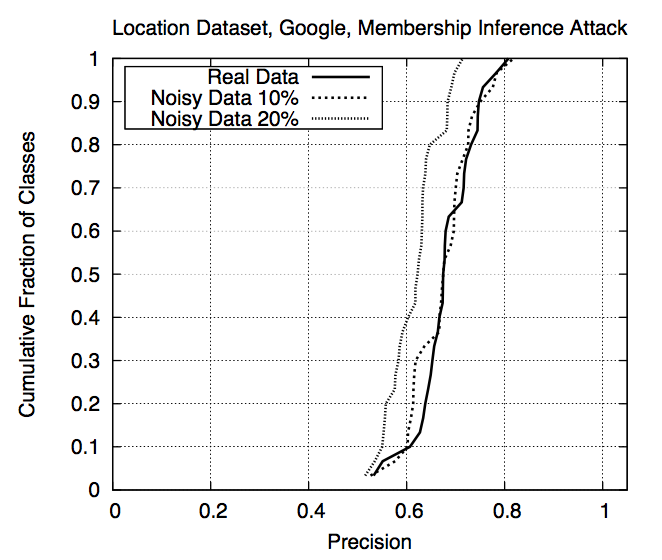
| Real data | 10% noise | 20% noise | |
|---|---|---|---|
| Precision | 0.678 | 0.666 | 0.613 |
| Recall | 0.98 | 0.99 | 1.00 |
- Concludes that attacks are robust even if assumptions about \(D^{training}_{target}\) are not very accurate
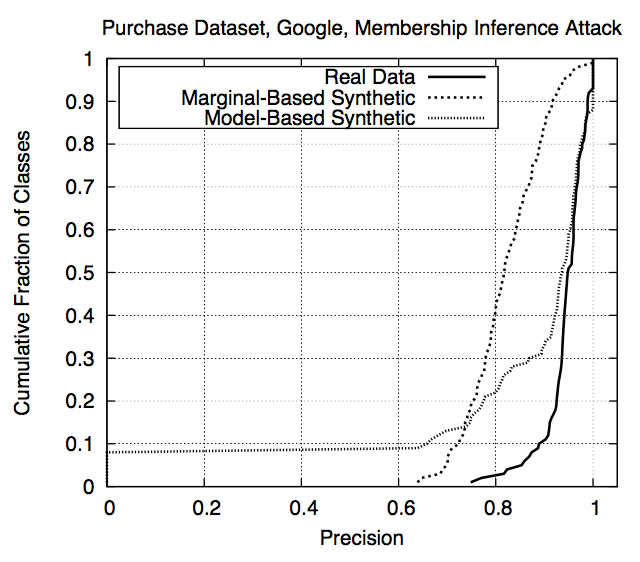
Real data vs synthetic data (Fig. 9) 🔗
- Overall precision: 0.935 on real data, 0.795 for marginal-based synthetics, 0.895 for model-based synthetics
- Much lower for marginal-based but still very high for most classes
- Dual behaviour for model-based: mostly very high but a few very low
- Because these classes make up < 0.6% of \(D^{training}_{target}\)
- Concludes attack can be trained with only black-box access
algorithm cannot synthesize representatives of these classes via search.
Why do the attacks work? 🔗
Overfitting from train-test gap 🔗
Models with higher generalizability are less vulnerable to membership inference attack
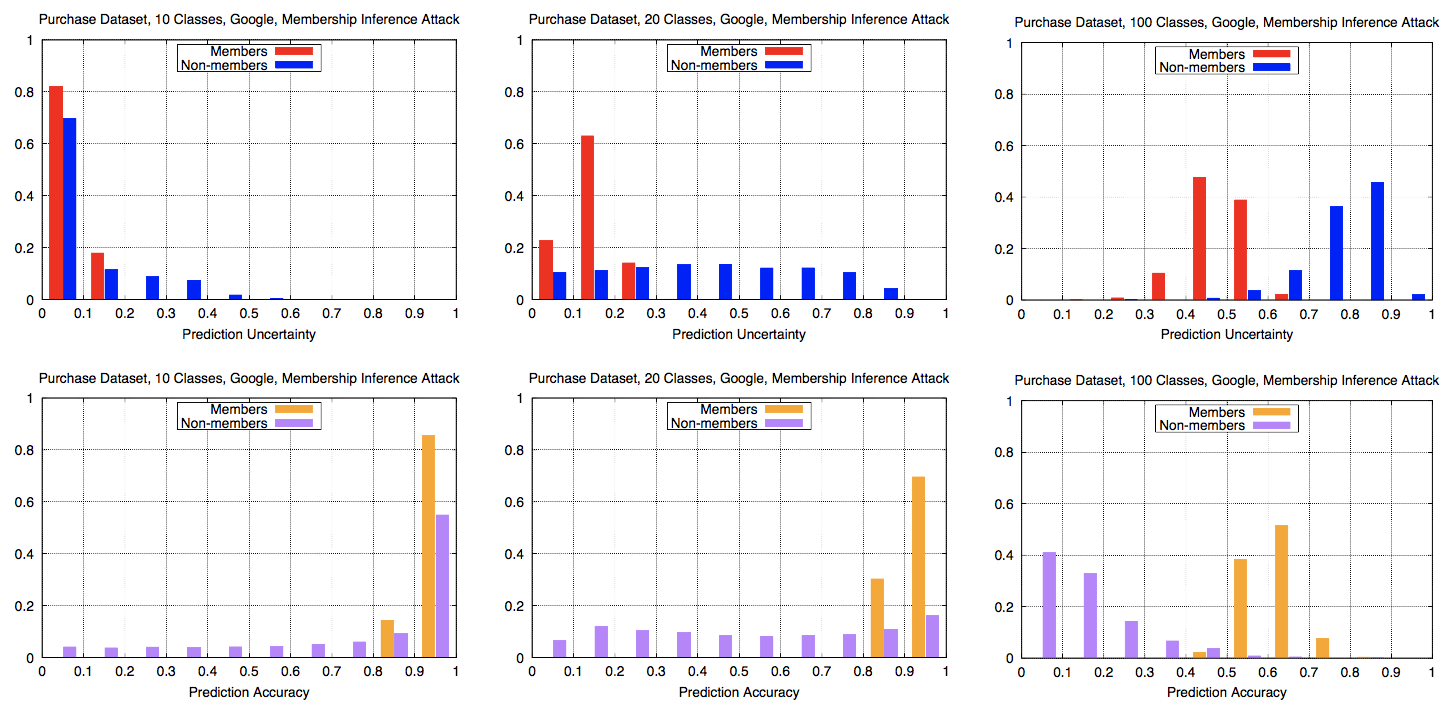
Relating accuracy and uncertainty of \(\mathbf{y}\) to membership 🔗
- Fig. 12: Differences between member vs non-member inputs’
- output metrics are more observable in the cases where attack is more successful (on purchase dataset with higher classes)
Mitigation strategies 🔗
- Restrict prediction vector \(\mathbf{y}\) to top \(k\) classes
- Round \(\mathbf{y}\) to \(d\) floating point digits
- Increase entropy of \(\mathbf{y}\) by increasing normalizing temperature \(t\) of softmax layer
- Use \(L_2\) -norm regularization with various factors \(\lambda\)
Evaluation of strategies 🔗
- Target model’s prediction accuracy maintained or improved (regularization)
- Unless regularization \(\lambda\) too large–need to be careful
- Nevertheless, regularization seems necessary and useful both for generalizing and decreasing information leakage
- Not just \(L_2\) -norm; dropout also shown to strengthen privacy guarantees
- Overall, attack is robust against mitigation strategies
- Restriction to top \(k=1\) class is not enough, as members and non-members are mislabeled differently
Conclusion 🔗
- First membership inference attack against machine learning models
- Shadow training technique using noisy data, or synthetic data without prior knowledge of \(D^{training}_{target}\)
Related work in data privacy threats in ML 🔗
Model inversion 🔗
- Authors took Fredrikson (2015), ran model inversion on CIFAR-10.
- If images in a class are diverse, “reconstructions” from model inversion are semantically meaningless
- Model inversion produces an average of a class and does not reconstruct any specific image, nor infer membership

Privacy-preserving machine learning 🔗
- ❎ Secure multiparty computation (SMC), or training on encrypted data, would not mitigate inference attacks
- ✅ Differential private models are, by construction, secure against the attack (this Friday)
ML Models that Remember Too Much (MTRTM) 🔗
- If this paper is a “side channel”, MTRTM is like a “covert channel”
- Malicious training algorithm intentionally designed to leak information
- Differences
- Extent of information leakage: Membership inference only vs up to 70% of corpus
- Relies on low generalizability of \(f\) vs. aims for high generalizability
Commentary 🔗
- 👍 Simplicity, intuition, many experiments, novelty
- Good evaluation and synthesis of related work
- Pick fewer binary datasets, attacks mostly performed quite poorly because of reasons mentioned (not enough signal for attack to extract useful membership information)
- Should have more real-valued features in datasets
- Why choose CIFAR to have locally-hosted target model? Because they have the largest training set? Would like to understand more of the reasons behind certain choices made.
- Some missing/hard-to-find information, e.g. in Fig. 12, which method used for shadow training data (to explain low prediction confidence for Google membership )
Commentary 🔗
- Why the higher the training dataset, the lower the precision, both overall (Fig. 1) and within each class (Fig. 11)? More overfitting, more signals…?
- Empirical CDF diagrams are a little confusing
- Why 10% and 20% noise, is that realistic? 20% a lot worse than 10% as well.
- Should the “out” data records for \(f_{attack}\) not all belong in the test set of the shadow models? Does it matter?
- Can you synthesize an adversarial example accidentally with model-based synthesis, and would it matter?
Discussion topics 🤔 🔗
- Realistic applications
- Do the paper’s results have “substantial practical privacy implications”?
- Or is this approach more practically useful as an evaluation metric, if lack of information leakage correlates to how well a model is regularized/generalizes?
- Also to measure effectiveness of privacy preserving techniques
- When should ML service providers be held accountable for training their models in a privacy-preserving manner?
- Having more generalizable models will both increase privacy and utility. Is this the root characteristic of a good ML model?
Discussion topics 🤔 🔗
- Scalability with number of classes, train a different \(f_{attack}\) for each class label \(y\).
- Also mode-based data synthesis method needs possibly many queries, especially as the size of the possible input space grows
- How to extend to regression models?
- How do differences in model structures affect information leakage?