Neural Ordinary Differential Equations 🐰🦊

Presented by Christabella Irwanto

Neural ODE

  • A new model class chen18_neural_ode, can be used as
    • Continuous-depth residual networks
    • Continuous-time latent variable models
  • Propose continuous normalizing flows, generative model
  • Scalable backpropagation through ODE solver
  • Paper shows various proofs of concept

ODE? 😕

“In the 300 years since Newton, mankind has come to realize that the laws of physics are always expressed in the language of differential equations.”

  • Steven Strogatz
  • An ODE is an equation involving an unknown function \(y=f(t)\) and at least one of its derivatives \(y’, y''\) etc.
    • Univariate functions (“time”) vs partial DE’s with multivariate input
    • Solve ODE by finding satisfying function \(f\)
  • Useful whenever it’s easier to describe change than absolute quantity, e.g. in many dynamical systems (☢, 🏀, 💊)

Bunny example 🐇

rabbit-overpopulation_2019-09-11_12-50-04.jpg

  • Model system of dynamics with first-order ODE, \(B'(t) = \frac{dB}{dt} = rB\)
    • \(B(t)\): bunny population at time \(t\)
    • \(r\): growth rate of new bunnies for every bunny, per \(\Delta t\)

Visualize ODE

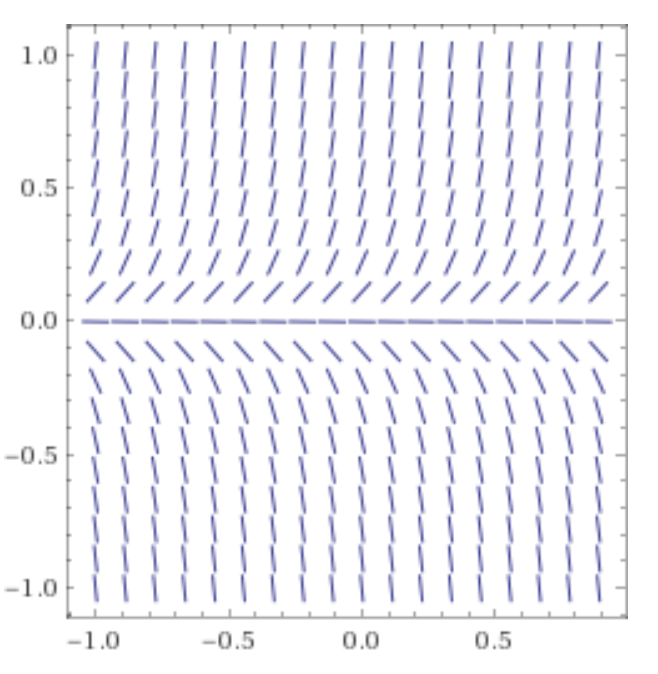
screenshot_2019-09-09_13-37-00.png

Slope field of derivative for each \((B, t)\)

Solve ODE

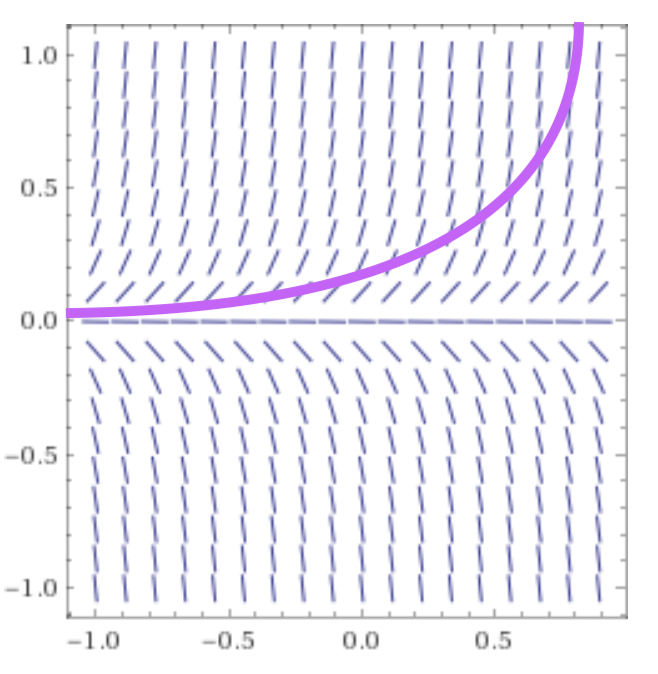
screenshot_2019-09-09_13-37-00-copy.png

  • Analytical solution via integration is \(B(t) = B(t_0)e^{rt}\)
  • Known initial value \(B(t_0)\)

Numerical ODE solver

  • Not all ODE’s have a closed form function satisfying it
    • Even if so, it’s very hard finding solutions
  • We have to numerically solve the ODE
    • Euler’s method, Runge-Kutta methods

Enter neural networks

  • Regular neural networks transform input with a series of functions \(f\),

\(\mathbf{h}_{t+1} = f(\mathbf{h}_t)\)

  • Each layer introduces error that compounds
  • Mitigate this by adding more layers, and limit the complexity of each step
  • Infinite layers, with infinitesimal step-changes?

Resnet

  • Instead of \(\mathbf{h}_{t+1} = f(\mathbf{h}_t)\), learn \(\mathbf{h}_{t+1} = \mathbf{h}_t + f(\mathbf{h}_t, \theta_t)\)
  • Similarly, RNN decoders and normalizing flows build complicated transformations by chaining sequences
  • Looks like Euler discretization of continuous transformation

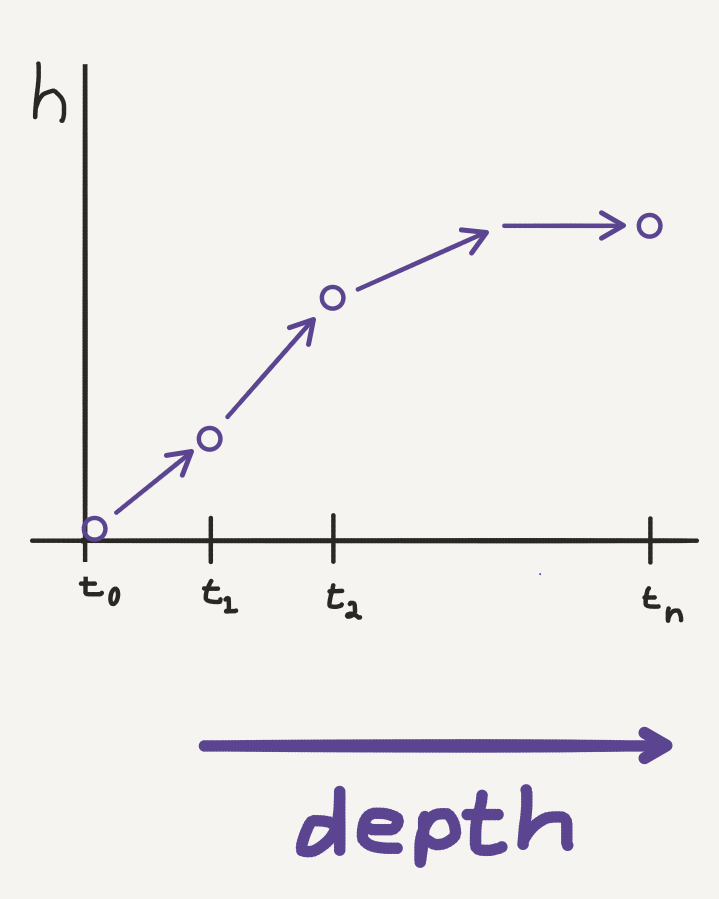
discrete_hidden_state_2019-09-11_14-15-45.png

Image from Jonty Sinai

Neural ODE

  • \(\mathbf{h}_{t+1} = \mathbf{h}_t + f(\mathbf{h}_t, \theta_t)\)
  • In the continuous limit w.r.t. depth \(t\), parameterize hidden state dynamics with an ODE specified by a neural network:
    • \(\frac{d\mathbf{h}(t)}{dt} = f(\mathbf{h}(t), t, \theta)\), where neural network \(f\) has parameters \(\theta\)
  • Function approximation now over a continuous hidden state dynamic

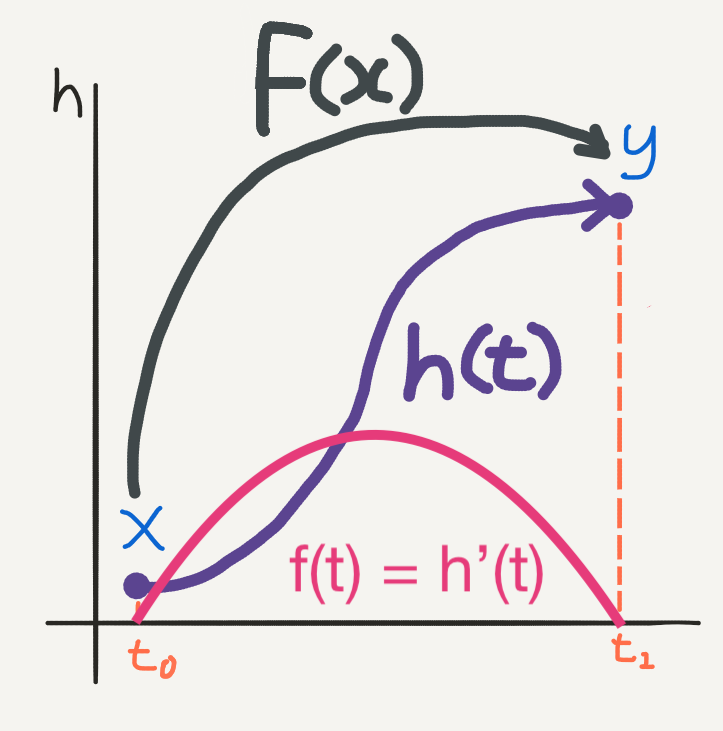
neural_ode_func_approx_2019-09-11_14-29-24.png

Image from Jonty Sinai

Resnet vs neural ODE

ode_networks_1_2019-09-11_12-44-23.png

Forward pass

  • 🐰 Evaluate \(\mathbf{h}(t_1)\) by solving the integral
    • \(\mathbf{h}(t) = \int f(t, \mathbf{h}(t), \theta_t)dt\)
  • If we use Euler’s method, we get exactly the residual state update!

neural_ode_func_approx_2019-09-11_14-29-24.png

Numerical ODE solver

  • Paper solves ODE initial value problems numerically with implicit Adams method
    • Not unconditionally stable
    • Current set of PyTorch ODE solvers only applicable to (some) non-stiff ODEs
  • Without a reversible integrator (implicit Adams is not reversible), method drifts from the true solution doing a backwards integration

Advantages

  • Use existing efficient solvers to integrate neural network dynamics
  • Memory cost is \(O(1)\) due to reversibility of ODE net
  • Tuning ODE solver tolerance gives trade-off between accuracy and speed
    • More fine-grained tuning,versus using lower precision floating point numbers

screenshot_2019-09-11_15-23-28.png

Backward pass

  • Output (hidden state at final depth) is used to compute loss
\begin{equation} L(\mathbf{z}(t_1)) = L\left( \mathbf{z}(t_0) + \int_{t_0}^{t_1} f(\mathbf{z}(t), t, \theta)dt \right) = L(\textrm{ODESolve}(\mathbf{z}(t_0), f, t_0, t_1, \theta)) \end{equation}
  • Scalable backpropagation through ODE solver with adjoint method
    • Vectorization to compute multiple derivatives in single call

How to train?

  • Standard reverse mode chain rule equations in backprop
  • Take continuous time limit of chain rule to recover the adjoint sensitivity equations

screenshot_2019-09-11_14-07-08.png

Adjoint sensitivity

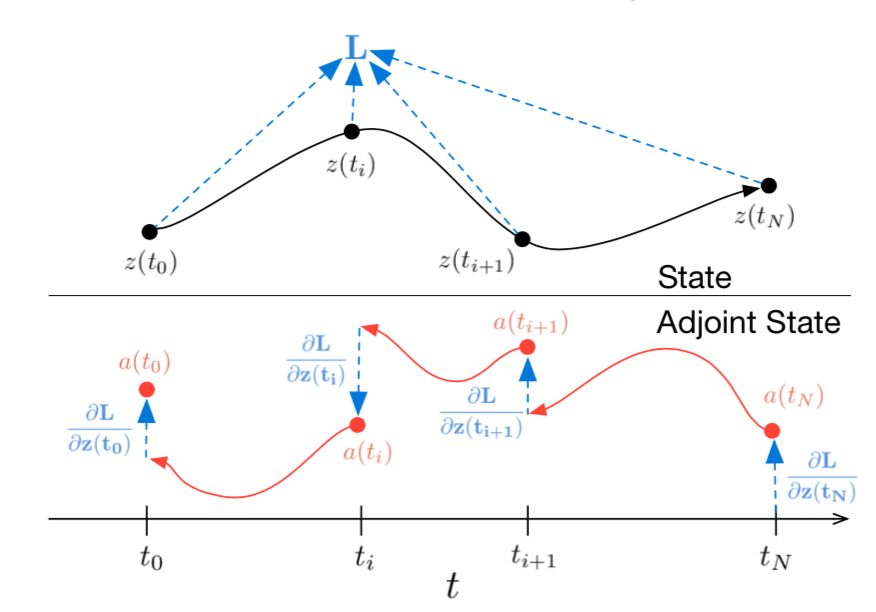
screenshot_2019-09-11_15-39-14.png

  • Reverse-mode differentiation of an ODE solution
  • Solving for adjoint state with same ODE solver used in forward pass

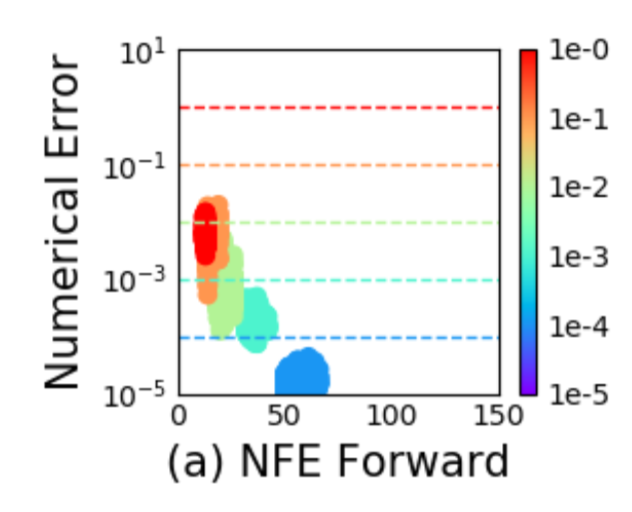
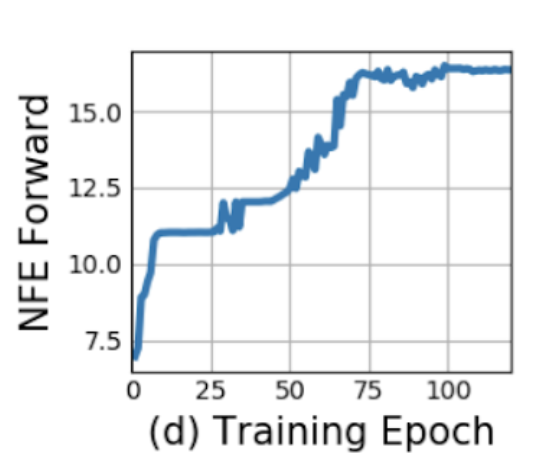
Results of ODE-Net vs Resnet

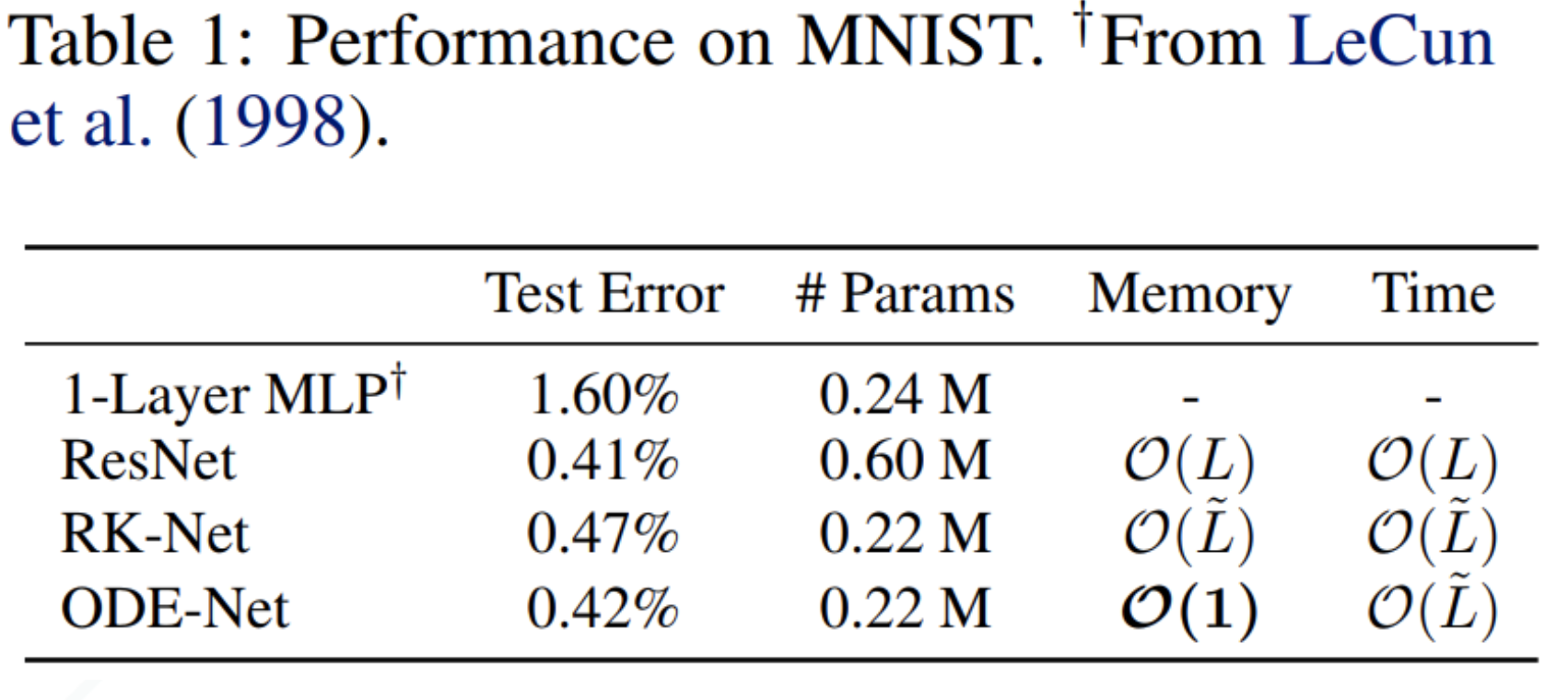
screenshot_2019-09-11_15-40-28.png

  • Fewer parameters with same accuracy
  • However, harder to train, tricky to implement mini-batching
  • Can't control the training time cost, computational complexity increases

screenshot_2019-09-11_15-41-21.png

Generative latent time-series model

  • Continuous-time approach to modeling time series

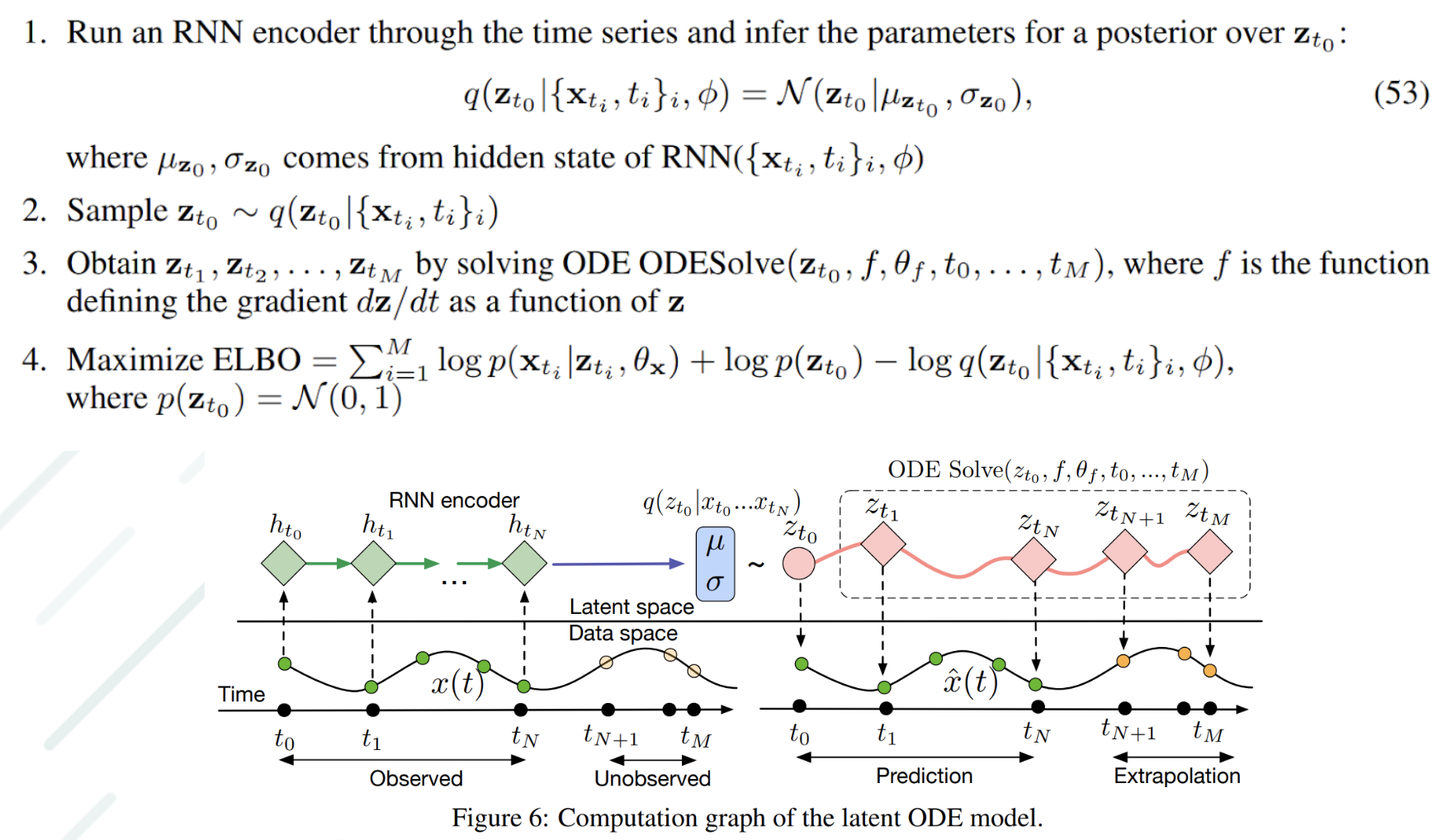
screenshot_2019-09-11_15-44-23.png

Results of experiments

  • Spiral dataset at irregular time intervals, with Gaussian noise

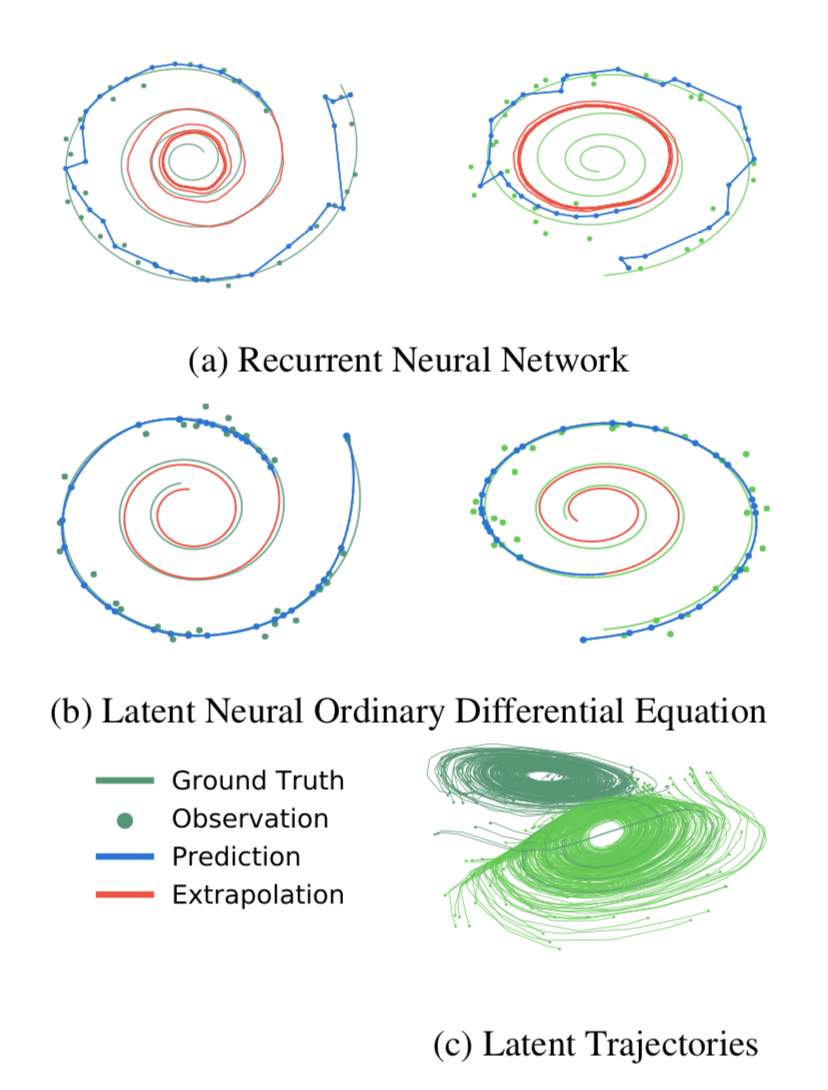
screenshot_2019-09-11_15-46-55.png

Advantages

  • For supervised learning, its main benefit is extra flexibility in the speed/precision tradeoff.
  • For time-series problems, allow handling of data at irregular intervals

Normalizing flows

  • Normalizing flows define a parametric density by iteratively transforming Gaussian sample:
\begin{align} z_0 &\sim Normal(0, I) \\ z_1 &= f_0(z_0) \\ … \\ x &= f_t(z_t) \end{align}
  • Use the change of variables formula to compute p(x): \(log p(z_{t+1}) = log p(z_t) - log | det \frac{df(z_t)}{dz_t} |\)
  • Paper proposes continuous-time version, Continuous NF
  • Derived continuous-time analogue of change of variables formula:

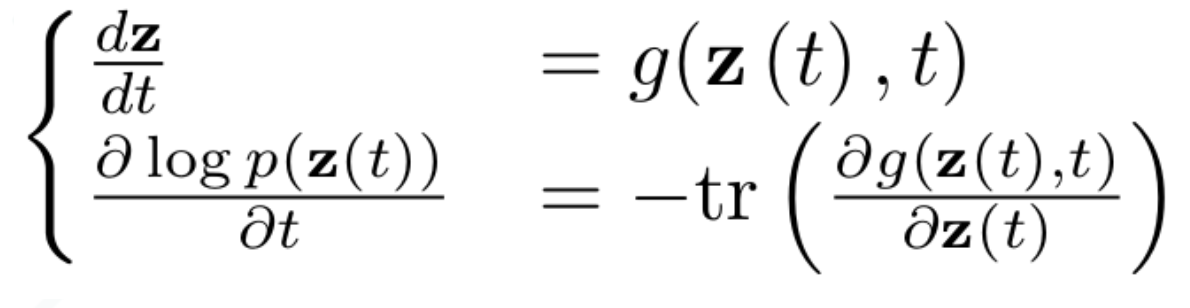
screenshot_2019-09-11_16-01-36.png

Results

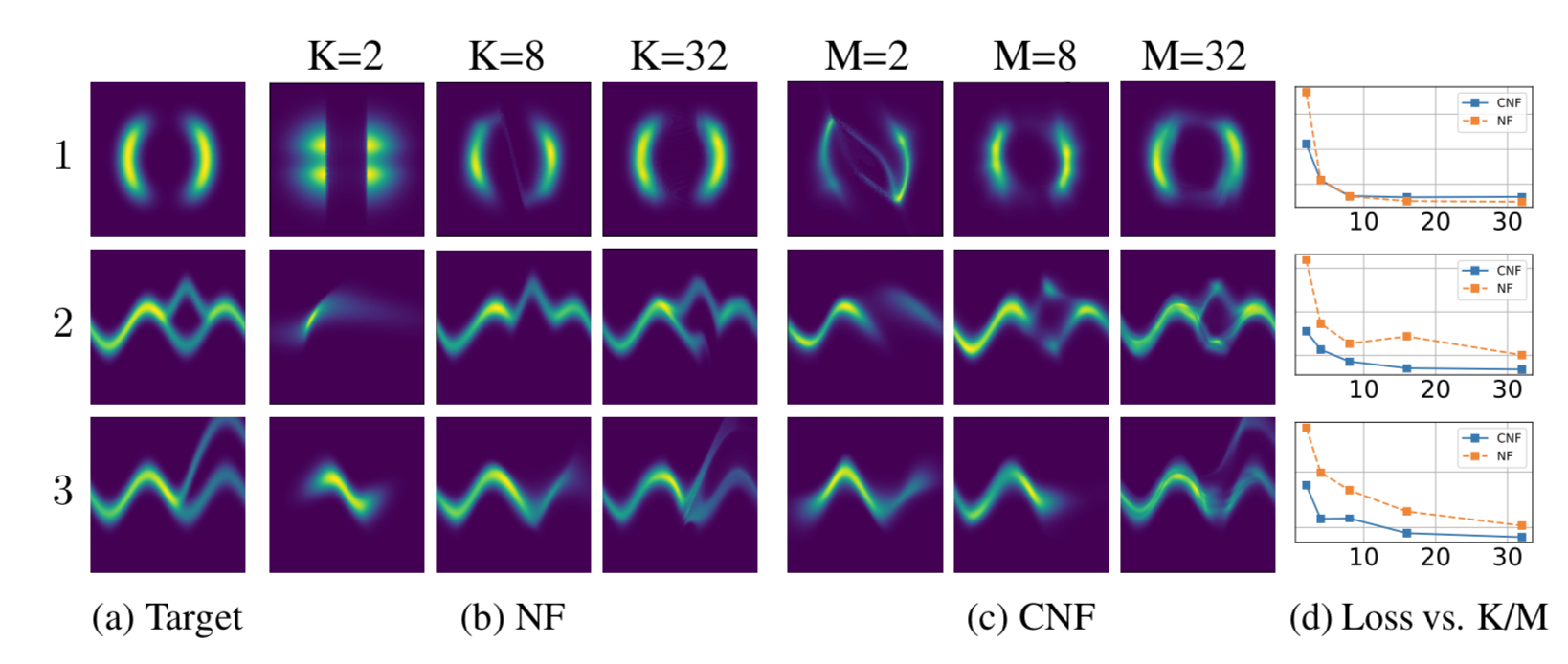
screenshot_2019-09-11_16-14-38.png

  • Compare Continuous NF to NF family of models on density estimation, image generation, and variational inference
  • Achieve state-of-the-art among exact likelihood methods with efficient sampling, in follow-up paper grathwohl18

Pros and cons

screenshot_2019-09-11_16-49-50.png

  • 4-5x slower than other methods (Glow, Real-NVP)

Summary

  • New and novel application of differential equation solvers as part of a neural net
  • Idea of Resnet/RNN as an Euler discretization is a neat solution
  • Much work can be done on both numerical differential equation and ML side

References

Code:

Blogposts

For adjoint sensitivity:

Original content from author(s)

Bibliography

  • [chen18_neural_ode] Ricky Chen, Yulia Rubanova, Jesse, Bettencourt & David Duvenaud, Neural Ordinary Differential Equations, , (2018).
  • [grathwohl18] Will Grathwohl, Ricky Chen, Jesse Bettencourt, Ilya Sutskever & David Duvenaud, FFJORD: Free-form Continuous Dynamics for Scalable Reversible Generative Models, , (2018).