“Meta-Learning in Neural Networks: A Survey” (Hospedales et al., 2020) has the most well-written, up-to-date, and comprehensive view of meta-learning I have encountered so far. It also covers applications such as §bayesian_meta_learning (in Section 5.5), and provides a clear high-level problem formulation to situate recent meta-learning approaches within, such as §neural_processes, §MAML, §fortuin19_deep_mean_gauss_proces.
For a quick primer on meta-learning, concrete examples of it, and recent Bayesian approaches framed within this survey’s high-level problem formulation, see §bayesian_meta_learning.
New taxonomy 🔗
The survey introduces a new breakdown of meta-learning along three independent axes: meta-representation, meta-optimizer and meta-objective.
Old taxonomy 🔗
Most work (Rusu et al., 2018) and articles (e.g. the popular Lil’Log blogpost by Lilian Weng, BAIR blogpost, Borealis AI series) used a three-way taxonomy across optimization-based methods, model-based (or black-box) methods, and metric-based (or non-parametric) methods.
[However,] the common breakdown reviewed above does not expose all facets of interest and is insufficient to understand the connections between the wide variety of meta-learning frameworks available today.
- We were approaching the limits of the flexibility of this taxonomy.
- It was starting to get messy as people came up with hybrid approaches, mixing and matching components of optimization-based, black-box, and metric-based methods:
- LEO (Rusu 19): gradient descent on an embedding that produces a set of parameters, combines all 3 approaches
- Proto-MAML (Triantafillou 19): like MAML (optimization) but initialize last layer as linear classifier equivalent to ProtoNets (Prototypical Networks are metric-based)
- CAML (Jiang 19): both black-box and runs gradient descent on parameters (optimization)
New taxonomy 🔗
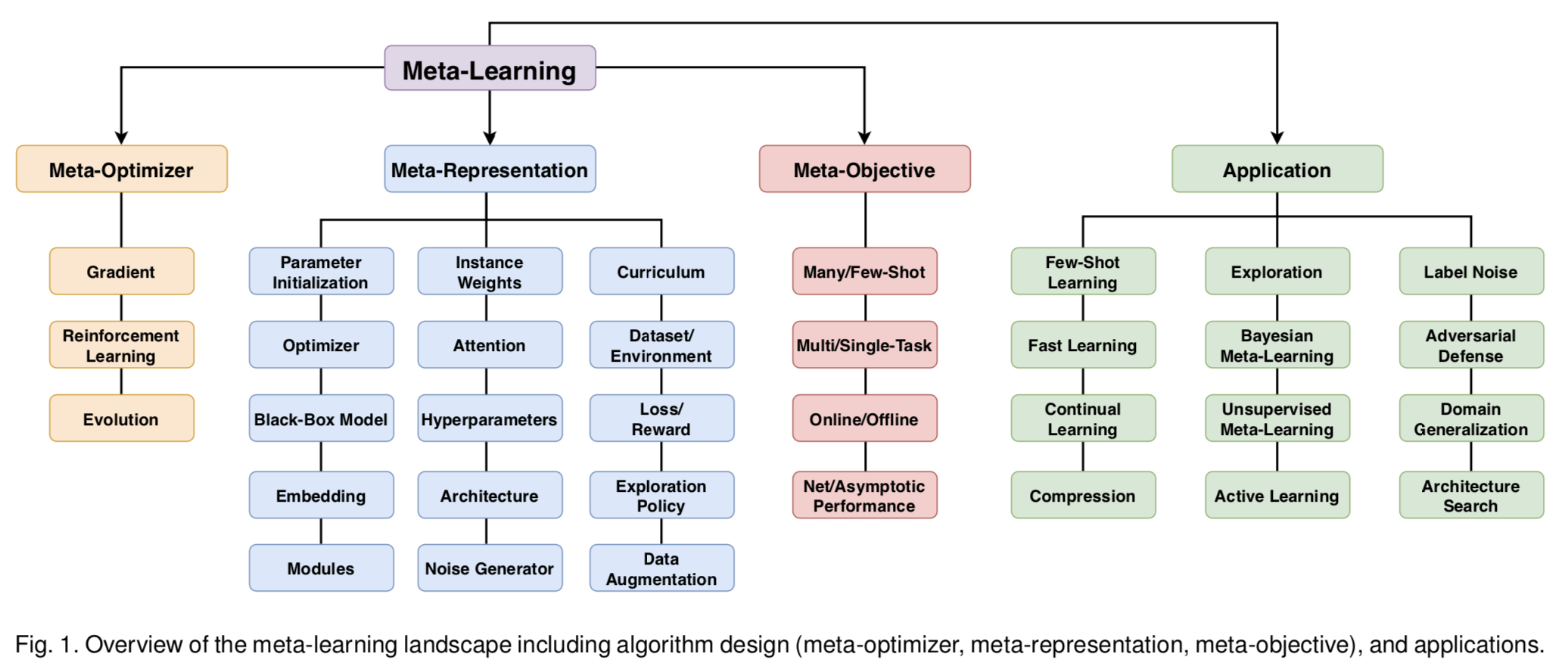
Figure 1: Taxonomy from Figure 1 in Hospedales et al. (2020).
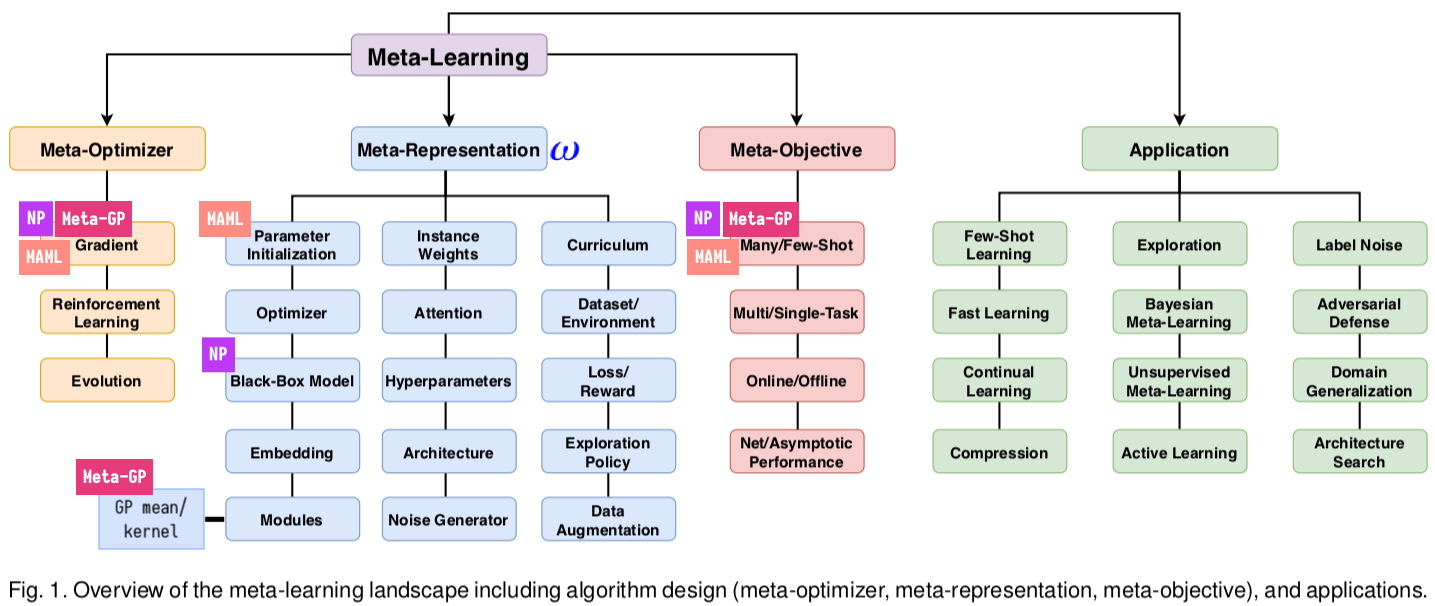
Figure 2: Situating NP, MAML, and meta-learning GP within the broader context of meta-learning, as given by Figure 1 in Hospedales et al. (2020).
Applications 🔗
In this section we discuss the ways in which meta-learning has been exploited – in terms of application domains such as computer vision and reinforcement learning and cross-cutting problems such as architecture search, hyper-parameter optimization, Bayesian and unsupervised meta-learning
Opinions 🔗
- The paper has a very useful taxonomy and review of existing literature.
- Doesn’t include a thread of work in meta-learning with GPs (Rothfuss et al., 2020), (Fortuin & R\“atsch, 2019), (Harrison et al., 2018)
- Quite related to Chelsea Finn’s lecture on Bayesian meta-learning (slides).
Practical motivation 🔗
Mentioned in passing:
applications also often naturally entail task families which meta-learning can exploit
meta- knowledge of a maze layout is transferable for all tasks that require navigating within the maze
Bibliography
Hospedales, T., Antoniou, A., Micaelli, P., & Storkey, A. (2020), Meta-learning in neural networks: a survey, CoRR. ↩
Rusu, A. A., Rao, D., Sygnowski, J., Vinyals, O., Pascanu, R., Osindero, S., & Hadsell, R. (2018), Meta-Learning With Latent Embedding Optimization, CoRR. ↩
Rothfuss, J., Fortuin, V., & Krause, A. (2020), Pacoh: bayes-optimal meta-learning with pac-guarantees, CoRR. ↩
Fortuin, V., & R\“atsch, Gunnar (2019), Deep mean functions for meta-learning in gaussian processes, CoRR. ↩
Harrison, J., Sharma, A., & Pavone, M. (2018), Meta-learning priors for efficient online bayesian regression, CoRR. ↩