Short(er) answer on StackOverflow.

An inductive bias allows a learning algorithm to prioritize one solution (or interpretation) over another, independent of the observed data (Battaglia et al., 2018). The word “inductive” comes from §inductive_reasoning in philosophy. Generally speaking, machine learning uses inductive reasoning, i.e. generalizes a target concept from limited training samples.

Examples in deep learning 🔗

Concretely speaking, the very composition of layers 🍰 in deep learning provides a type of relational inductive bias: hierarchical processing. The type of layer imposes further relational inductive biases:

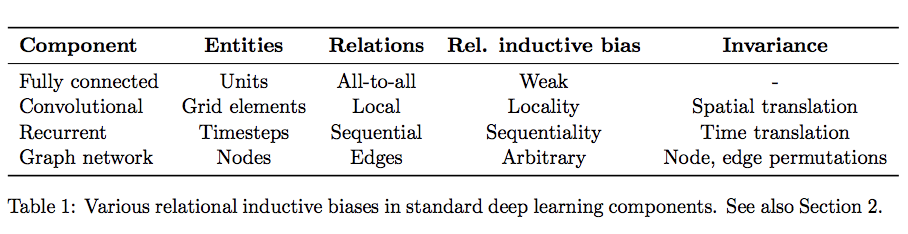Convolutional layers exploit spatial translational invariance and locality; recurrent layers exploit temporal invariance and locality.

If there is symmetry in the input space, exploit it.

(From Max Welling’s keynote talk on inductive bias at CoNLLL 2018.)

More generally, non-relational inductive biases used in deep learning are anything that imposes constraints on the learning trajectory, including:

• activation non-linearities,
• weight decay,
• dropout,
• batch and layer normalization,
• data augmentation,
• training curricula,
• optimization algorithms,

Examples outside of deep learning 🔗

In a Bayesian model, inductive biases are typically expressed through the choice and parameterization of the prior distribution. Adding a Tikhonov regularization penalty to your loss function implies assuming that simpler hypotheses are more likely (Occam’s razor). The inductive bias obtained through multi-task learning encourages the model to prefer hypotheses that explain more than one task. In k-nearest neighbors, kernel methods, Gaussian processes etc., inductive biases cases that are near each other tend to belong to the same class.

The role of inductive bias 🔗

The stronger the inductive bias, the better the sample efficiency–this can be understood in terms of the bias-variance tradeoff. Many modern deep learning methods follow an “end-to-end” design philosophy which emphasizes minimal a priori representational and computational assumptions, which explains why they tend to be so data-intensive. On the other hand, there is a lot of research into baking stronger relational inductive biases into deep learning architectures, e.g. with graph networks.

Bibliography

Battaglia, P. W., Hamrick, J. B., Bapst, V., Sanchez-Gonzalez, A., Zambaldi, V., Malinowski, M., Tacchetti, A., … (2018), Relational inductive biases, deep learning, and graph networks, CoRR. ↩