
“I can’t believe it’s not Bayesian” - Chelsea Finn, ICML 2019 meta-learning workshop
This post is also available as Reveal.JS slides 📺 (press the right arrow key \(\rightarrow\) to advance).
Agenda 🔗
- Meta-learning: why, what, and how?
- Using Bayesian principles in meta-learning.
- A few examples, fast and furious edition:
- Model-agnostic meta-learning (MAML) as hierarchical Bayes
- Neural Process (NP)
- Deep meta-learning GPs
Why meta-learning? 🔗
- It is more human/animal-like 👪🐕: humans can learn from a rich ensemble of partially related tasks, extracting shared information from them and applying that on new tasks with few samples (Lake et al., 2016)
- Learning-to-learn has been studied in cognitive science (Lake et al., 2015) and psychology (Hospedales et al., 2020), (Griffiths et al., 2019),
- It seeks to address data-hungry 💸 supervised deep learning.
- Data efficiency using prior knowledge transferred from related tasks.
- Successful applications in few-shot image recognition, data efficient reinforcement learning (RL), and neural architecture search (NAS).
- EfficientNet’s, current SoTA beating ResNet, are found via NAS.
What is meta-learning? 🔗
- Actually, you already know it—it’s a broad framework that encompasses a commonplace machine learning (ML) practice: hyperparameter search.
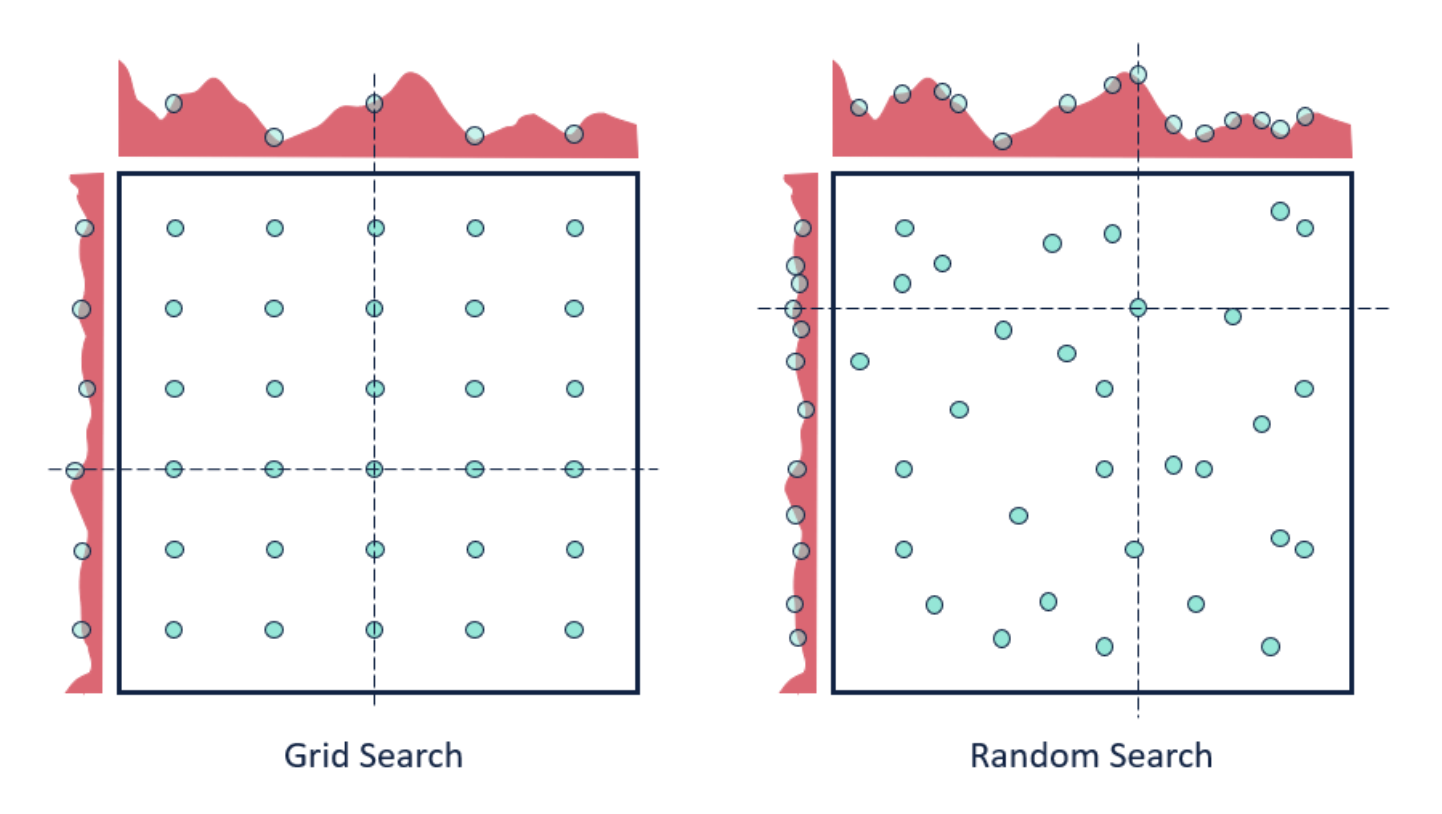
Figure 1: Hyperparameter searches (image source)
But really, what is it? 🔗
- Difficult to define, as it has been used in different ways, but a good start is:
The salient characteristic of contemporary neural-network meta-learning is an explicitly defined meta-level objective, and end-to-end optimization of the inner algorithm with respect to this objective (Hospedales et al., 2020)
Conventional vs meta-learning 🔗
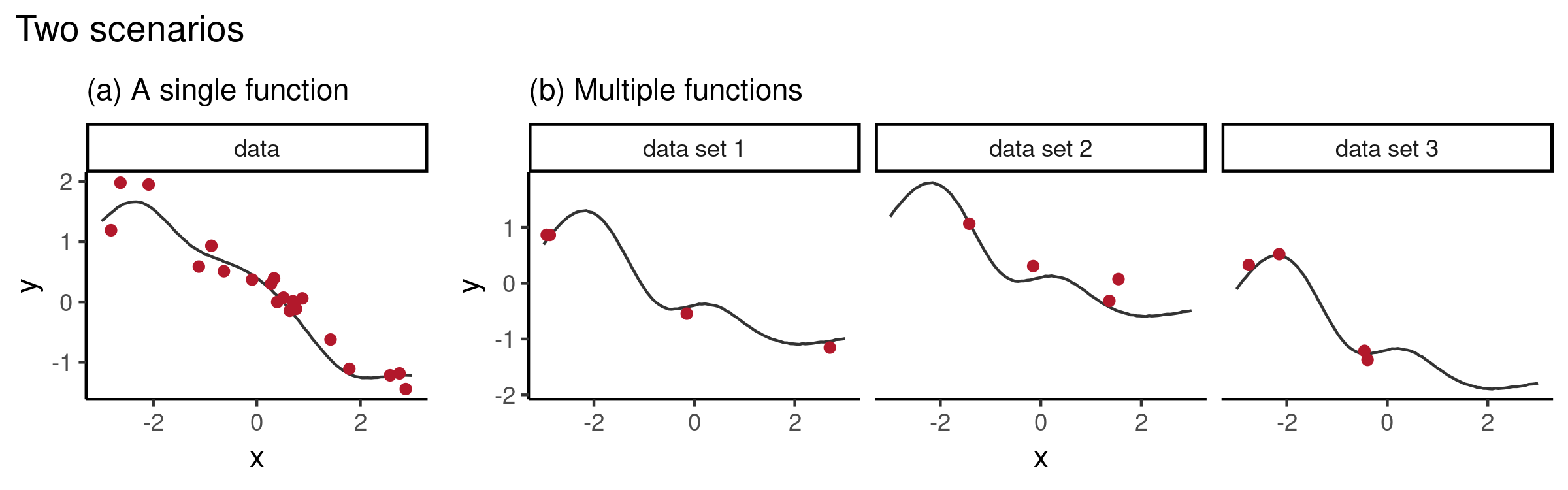
Figure 2: Conventional vs meta-learning for 1D function regression (image source)
- a): Single dataset \(\mathcal{D} = (x, y)_{i=1}^n, y_i = f_{\theta, \color{blue}{ \omega}}(x_i )\)
- Learn \(f_{\theta, \color{blue}{ \omega}}:\mathcal{X} \rightarrow \mathcal{Y}\) that is explicitly parameterized by \(\theta\) (e.g. neural network weights) and implicitly pre-specified by \(\color{blue}{\text{a fixed } \omega}\) (e.g. learning rate, optimizer).
- Optimize for \(\theta^* = \arg \min_\theta \mathcal{L}_\theta(\mathcal{D}; \theta, \color{blue}{\omega})\).
- b): Dataset of datasets \(\{\mathcal{D}_t \}_{t=1}^{3}\) from task distribution \(p(\mathcal{T}), \mathcal{T} = {\mathcal{D}, \mathcal{L}}\).
- Objective: \(\color{blue}{\text{A learnable }\omega}\) is optimized over \(p(\mathcal{T})\), i.e. \(\displaystyle \color{blue}{\omega^*} = \min _{\color{blue}{\omega}} \underset{\tau \sim p(\mathcal{T})}{\mathbb{E}} \mathcal{L}(\mathcal{D} ; \color{blue}{\omega})\).
- Meta-knowledge \(\color{blue}{\omega}\) specifies “how to learn” \(\theta\).
- E.g. Shared meta-knowledge \(\color{blue}{\omega}\) can encode the family of sine functions (everything but phase and amplitude) while \(\theta\) encodes the phase and amplitude.
Two phases of meta-learning methods 🔗
- Generally split into two phases (Hospedales et al., 2020):
- Meta-training on \(\mathscr{D}_{\text {source}}=\left\{\left(\mathcal{D}_{\text {source}}^{\text {train}}, \mathcal{D}_{\text {source}}^{\text {val}}\right)^{(i)}\right\}_{i=1}^{M}\) entails \(\omega^{*}=\arg \max _{\omega} \log p\left(\omega | \mathscr{D}_{\text {source }}\right)\)
- Meta-testing (online adaptation) on \(\mathscr{D}_{\text {target}}=\left\{\left(\mathcal{D}_{\text {target}}^{\text {train}}, \mathcal{D}_{\text {target}}^{\text {test}}\right)^{(i)}\right\}_{i=1}^{Q}\) entails \(\theta^{*(i)}=\arg \max _{\theta} \log p\left(\theta | \omega^{*}, \mathcal{D}_{\text {target}}^{\text {train}}(i)\right)\). Evaluation done on \(\mathcal{D}_{\text {target}}^{\text {test}}\).

Figure 3: “3-way-2-shot” (few-shot) classification. Each source task’s train set contains 3 classes of 2 examples each (Vinyals et al., 2016). Image modified from Borealis AI blogpost.
MAML: Model-agnostic meta-learning 🔗
- MAML (Finn et al., 2017) is a simple and popular approach of two phases:
- During meta-training (bold line), learn a good weight initialization \(\color{blue}{\omega^*}\) for fine-tuning on target tasks.
- During meta-testing (dashed lines), find the optimal \(\theta^*_i\) for each new task \(i\).
- Good performance
- MAML substantially outperformed other approaches on few-shot image classification (Omniglot, MiniImageNet2), and improved adaptability of RL agent.
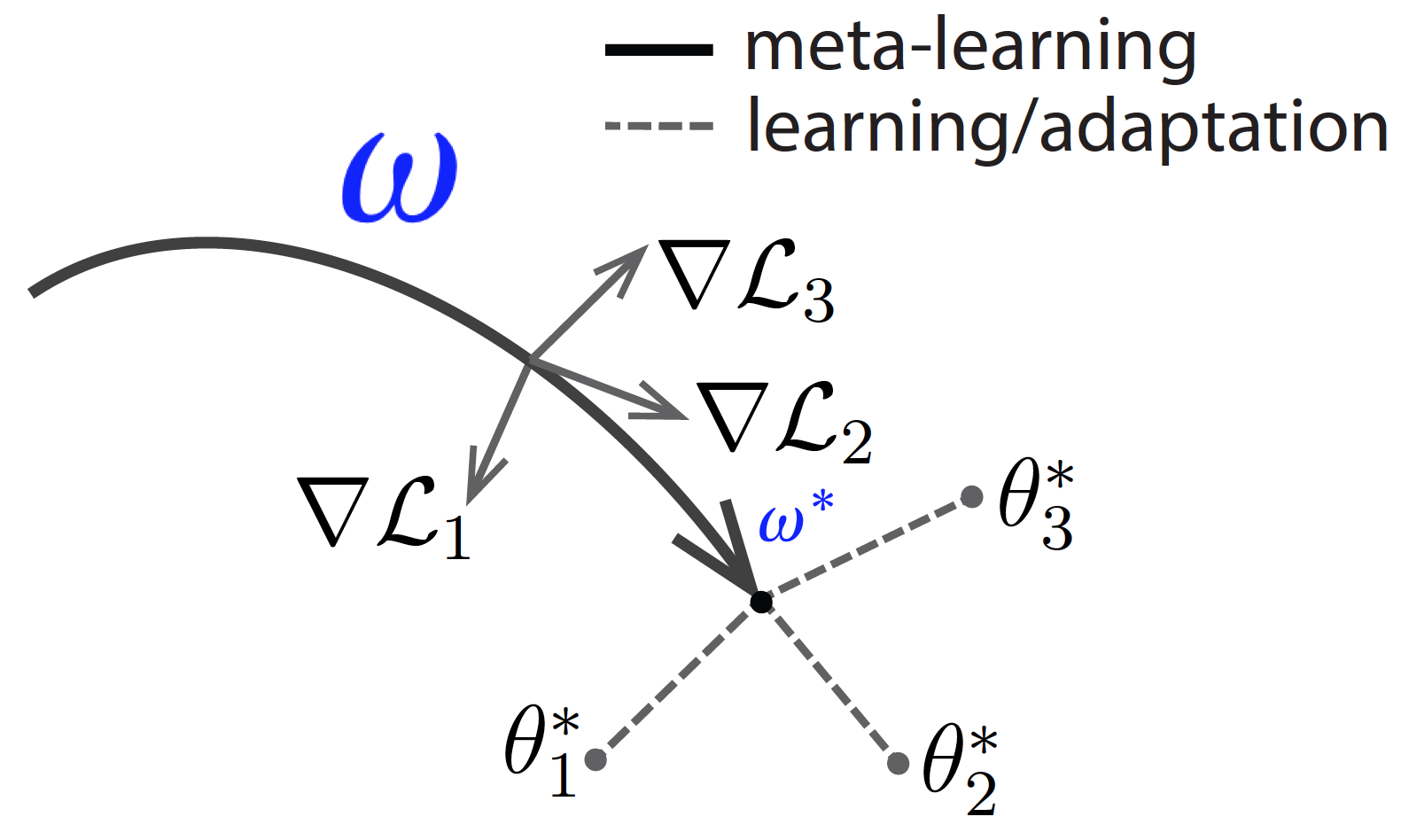
Figure 4: Visualized MAML (image modified from BAIR blogpost).
A little side-note 🔗

- Feature reuse, not rapid learning, is the dominant component in MAML.
A little side-note: “Rapid Learning or Feature Reuse? Towards Understanding the Effectiveness of MAML” 🔗
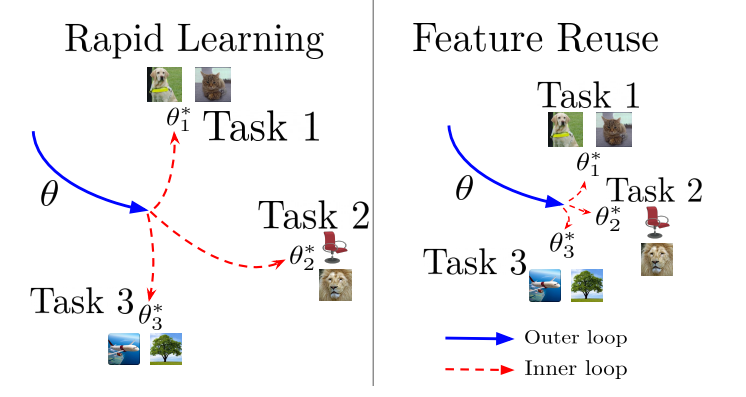
Figure 5: Rapid learning entails efficient but significant change from \(\color{blue}{\omega^*}\) to \(\theta^*\); feature reuse is where \(\color{blue}{\omega^*}\) already provides high quality representations. Figure 1 from the paper.
- Feature reuse, not rapid learning, is the dominant component in MAML.
- Used CCA and CKA to study the learnt representations.
- Led to a simplified algorithm, ANIL, which almost completely removes the inner optimization loop with no reduction in performance.
- Benchmark datasets (e.g. Omniglot, MiniImageNet2) are artifically segmented from the same dataset, hence it might be very easy to reuse features. Interesting to consider less similar tasks (e.g. Meta-dataset, Triantafillou et al. 2019).
Concrete examples of \(\color{blue}{\omega}\) and \(\theta\) 🔗
Conventional ML: \(\color{blue}{\text{fixed }\omega}\).
| Shared meta-knowledge \(\color{blue}{\omega}\) | Task-specific \(\theta\) | |
|---|---|---|
| NN | Hyperparameters (e.g. learning rate, weight initialization scheme, optimizer, architecture design) | Network weights |
Meta-learning: \(\color{blue}{\text{learnt }\omega}\) from \(\mathcal{D}_{\mathrm{source}}\).
| Shared meta-knowledge \(\color{blue}{\omega}\) | Task-specific \(\theta\) | |
|---|---|---|
| Hyperopt | Hyperparameters (e.g. learning rate) | Network weights |
| MAML | Network weights (initialization learnt from \(\mathcal{D}_{\mathrm{source}}\)) | Network weights (tuned on \(\mathcal{D}_{\mathrm{target}}\)) |
| NP | Network weights | Aggregated target context [latent] representation |
| Meta-GP | Deep mean/kernel function parameters | None (a GP is fit on \(\mathcal{D}_{\mathrm{target}}^{\mathrm{train}}\)) |
A \(\color{blue}{\omega}\) by any other name… 🌹 🔗
- \(\color{blue}{\omega}\) is shared/task-general parameters that work well across different tasks.
- Examples of parameterized task-general components include a metric space (Vinyals et al., 2016), an RNN (Duan et al., 2016), a memory-augmented NN (Santoro et al., 2016).
- Again, meta-knowledge \(\color{blue}{\omega}\) specifies “how to learn” \(\theta\).
- \(\color{blue}{\omega}\) is a starting inductive bias for new tasks from old tasks; equivalent to ‘learning a prior’.
- \(\implies\) There is a loose analogy between any meta-learning approach and hierarchical Bayesian inference (Griffiths et al., 2019).
- Bayesian inference generically indicates how a learner should combine data with a prior distribution over hypotheses
- Hierarchical Bayesian inference for meta-learning learns that prior through experience (data from related tasks).
Bayesian meta-learning 🔗
- Opens opportunities to (Griffiths et al., 2019):
- Translate cognitive science insights, which has focused on hierarchical Bayesian models (HBMs), to ML.
- Use probabilistic generative models from Bayesian deep learning toolbox for meta-learning.
- Useful for safety-critical few-shot learning (e.g. medical imaging), active learning, and exploration in RL (à la Marc Deisenroth’s talk on probabilistic RL).
MAML as a HBM 🔗
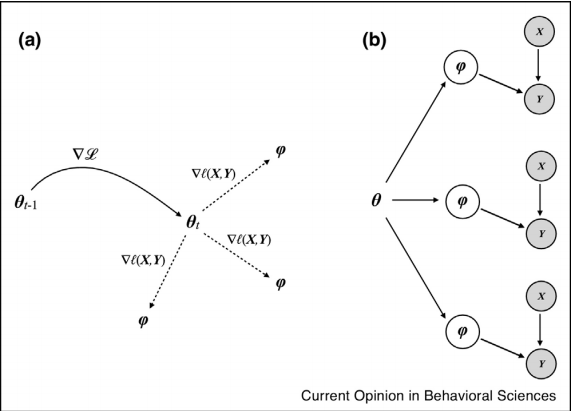
Figure 6: MAML and its corresponding probabilistic graphical model. Figure 2 from Griffiths et al. (2019).
- Grant et al. (2018) (Grant et al., 2018) show that:
- The few steps of gradient descent by the task-specific learners result in \(\theta^*\), which is an approximation to the Bayesian estimate of \(\theta\) for that task, with a prior that depends on the initial parameterization \(\color{blue}{\omega^*}\) .
- \(\implies\) Learning \(\color{blue}{\omega}\) is equivalent to learning a prior.
LVM + amortized VI for meta-learning 🔗
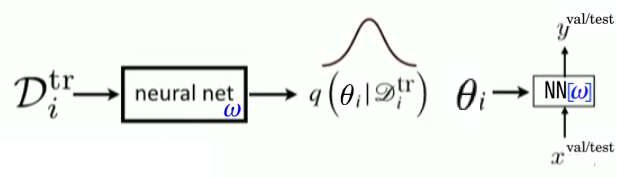
Figure 7: Same at meta-train \(\left(\mathcal{D}_{\text {source}}^{\text {train}}, \mathcal{D}_{\text {source}}^{\text {val}}\right)\) and meta-test \(\left(\mathcal{D}_{\text {target}}^{\text {train}}, \mathcal{D}_{\text {target}}^{\text {test}}\right)\) time.
- Standard VAE optimizes ELBO \(p(\mathbf{x}) \geq \text{ELBO} = \mathbb{E}_{\mathbf{z}\sim q_\phi(\mathbf{z}\vert\mathbf{x})} \left[ \log p_\theta(\mathbf{x}\vert\mathbf{z}) \right] - D_\text{KL}(q_\phi(\mathbf{z}\vert\mathbf{x}) \| p_\theta(\mathbf{z}))\)
- Neural Processes (Garnelo et al., 2018), Versa (Jonathan Gordon et al., 2019) etc. take inspiration from VAE for meta-learning by treating \(\theta\) as \(\mathbf{z}\).
- \(\log p\left(\mathbf{Y}_{T} \mid \mathbf{X}_{T}, \mathbf{X}_{C}, \mathbf{Y}_{C}\right) \geq \mathbb{E}_{q\left(\mathbf{z} \mid \mathbf{s}_{T}\right)}\left[\log p\left(\mathbf{Y}_{T} \mid \mathbf{X}_{T}, \mathbf{r}_{C}, \mathbf{z}\right)\right] - D_{\mathrm{KL}}\left(q\left(\mathbf{z} \mid \mathbf{s}_{C}, \mathbf{s}_{T}\right) \| q\left(\mathbf{z} \mid \mathbf{s}_{C}\right)\right)\)
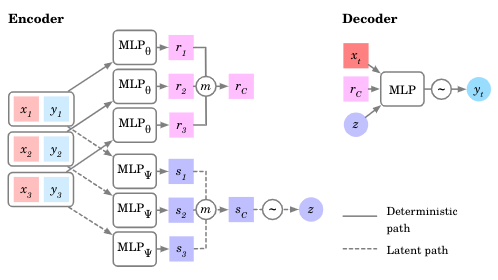
Figure 8: In an NP, meta-parameters \(\color{blue}{\omega}\) are the weights of the encoder and decoder NNs.
GPs for meta-learning 🔗
- Use a neural network for the mean or kernel function (Fortuin & R\“atsch, 2019)
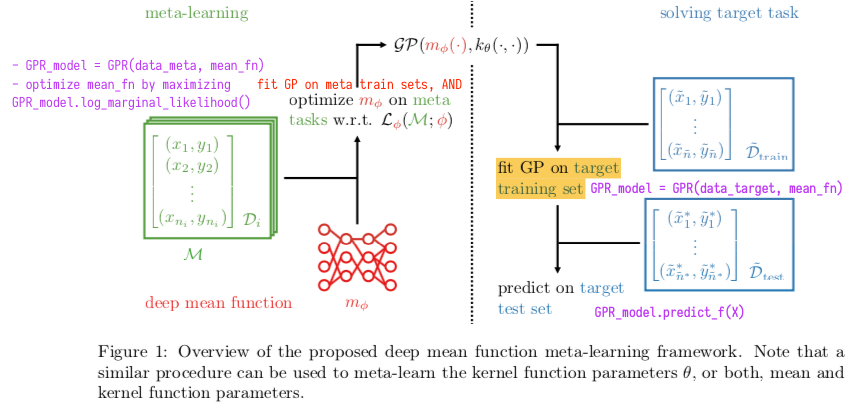
Figure 9: Figure 1 from Fortuin et al. (2019). Corresponding GPFlow code in purple.
What else can it be used for? 🔗
- RL agent trains on some mazes and is tested on unseen mazes generated by the same process (Duan et al., 2016), (Mishra et al., 2017)
Many methods and applications 🔗
We can situate NP, MAML, and meta-learning deep mean/kernel GP within the meta-learning taxonomy across 3 independent axes (Hospedales et al., 2020).
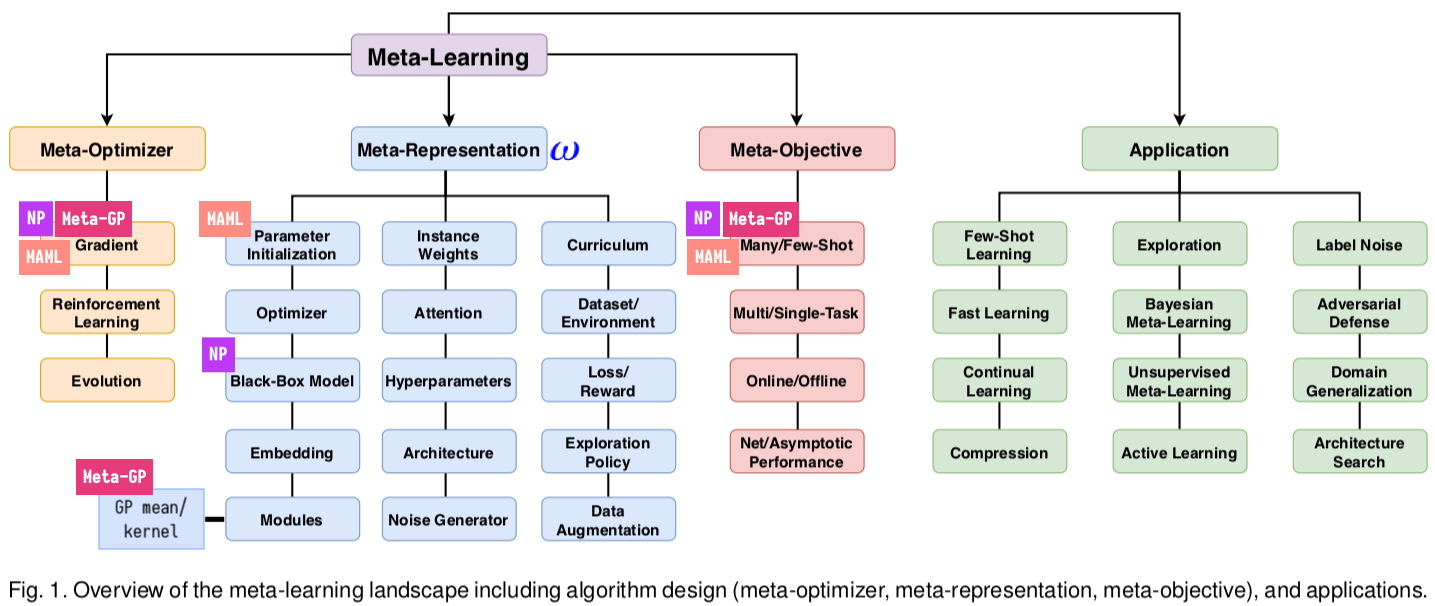
Figure 10: Taxonomy modified from Figure 1 in Hospedales et al. (2020).
Conclusion 🔗
- The core idea of meta-learning is to optimize a model over a distribution of learning tasks \(p(\mathcal{T})\), rather than just a single task, with the goal of generalizing to other tasks from \(p(\mathcal{T})\).
Recap of \(\color{blue}{\omega}\) and \(\theta\) 🔗
Conventional ML has fixed/pre-specified meta-knowledge \(\color{blue}{\omega}\).
| Shared meta-knowledge \(\color{blue}{\omega}\) | Task-specific \(\theta\) | |
|---|---|---|
| NN | Hyperparameters (e.g. learning rate, weight initialization scheme, optimizer, architecture design) | Network weights |
Meta-learning challenges this assumption by learning a prior on \(\color{blue}{\omega}\) from \(\mathcal{D}_{\mathrm{source}}\)
| Shared meta-knowledge \(\color{blue}{\omega}\) | Task-specific \(\theta\) | |
|---|---|---|
| Hyperopt | Hyperparameters (e.g. learning rate) | Network weights |
| MAML | Network weights (initialization learnt from \(\mathcal{D}_{\mathrm{source}}\)) | Network weights (tuned on \(\mathcal{D}_{\mathrm{target}}\)) |
| NP | Network weights | Aggregated target context [latent] representation |
| Meta-GP | Deep mean/kernel function parameters | None (a GP is fit on \(\mathcal{D}_{\mathrm{target}}^{\mathrm{train}}\)) \(\bigstar\) |
\(\bigstar\) In GPs, while the data is used at test time, no optimization is really done since GPs are nonparametric, i.e. there’s no (or infinite) parameters to explicitly learn for meta-test time.
Bibliography
Lake, B. M., Ullman, T. D., Tenenbaum, J. B., & Gershman, S. J. (2016), Building machines that learn and think like people, CoRR. ↩
Lake, B., Salakhutdinov, R., & Tenenbaum, J. (2015), [Human-level concept learning through probabilistic program induction](), Science. ↩
Hospedales, T., Antoniou, A., Micaelli, P., & Storkey, A. (2020), Meta-learning in neural networks: a survey, CoRR. ↩
Griffiths, T. L., Callaway, F., Chang, M. B., Grant, E., Krueger, P. M., & Lieder, F. (2019), [Doing more with less: meta-reasoning and meta-learning in humans and machines](), Current Opinion in Behavioral Sciences. ↩
Finn, C., Abbeel, P., & Levine, S., Model-agnostic meta-learning for fast adaptation of deep networks, In , International Conference on Machine Learning (ICML) (pp. 1126–1135) (2017). : . ↩
Vinyals, O., Blundell, C., Lillicrap, T., Wierstra, D., & others, , Matching networks for one shot learning, In , Advances in neural information processing systems (pp. 3630–3638) (2016). : . ↩
Duan, Y., Schulman, J., Chen, X., Bartlett, P. L., Sutskever, I., & Abbeel, P. (2016), Rl$^2$: fast reinforcement learning via slow reinforcement learning, CoRR. ↩
Santoro, A., Bartunov, S., Botvinick, M., Wierstra, D., & Lillicrap, T., Meta-learning with memory-augmented neural networks, In , International Conference on Machine Learning (ICML) (pp. 1842–1850) (2016). : . ↩
Grant, E., Finn, C., Levine, S., Darrell, T., & Griffiths, T. (2018), Recasting Gradient-Based Meta-Learning As Hierarchical Bayes, CoRR. ↩
Garnelo, M., Schwarz, J., Rosenbaum, D., Viola, F., Rezende, D. J., Eslami, S. M. A., & Teh, Y. W. (2018), [Neural Processes](), arXiv preprint: 1807.01622. ↩
Gordon, J., Bronskill, J., Bauer, M., Nowozin, S., & Turner, R. (2019), Meta-learning probabilistic inference for prediction, . ↩
Fortuin, V., & R\“atsch, Gunnar (2019), Deep mean functions for meta-learning in gaussian processes, CoRR. ↩
Mishra, N., Rohaninejad, M., Chen, X., & Abbeel, P., A simple neural attentive meta-learner, In , (pp. ) (2017} # booktitle # {Workshop on Meta-Learning, NeurIPS). : . ↩